Graham Scan Algorithm to find Convex Hull

Reading time: 25 minutes | Coding time: 10 minutes

Graham's Scan Algorithm is an efficient algorithm for finding the convex hull of a finite set of points in the plane with time complexity O(N log N). The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently.

It is named after Ronald Graham, who published the original algorithm in 1972.

Algorithm

In Jarvis’s Algorithm for Convex Hull. Worst case time complexity of Jarvis’s Algorithm is O(n^2). Using Graham’s scan algorithm, we can find Convex Hull in O(nLogn) time. Following is Graham’s algorithm

Let points[0..n-1] be the input array.

1. Find the bottom-most point by comparing y coordinate of all points. If there are two points with same y value, then the point with smaller x coordinate value is considered. Let the bottom-most point be P0. Put P0 at first position in output hull.

2. Consider the remaining n-1 points and sort them by polor angle in counterclockwise order around points[0]. If polor angle of two points is same, then put the nearest point first.

3 After sorting, check if two or more points have same angle. If two more points have same angle, then remove all same angle points except the point farthest from P0. Let the size of new array be m.

4. If m is less than 3, return (Convex Hull not possible)

5. Create an empty stack ‘S’ and push points[0], points[1] and points[2] to S.

6. Process remaining m-3 points one by one. Do following for every point ‘points[i]’
   4.1) Keep removing points from stack while orientation of following 3 points is not counterclockwise (or they don’t make a left turn).
   a) Point next to top in stack
   b) Point at the top of stack
   c) points[i]
   4.2) Push points[i] to S

7. Print contents of S

The above algorithm can be divided in two phases.

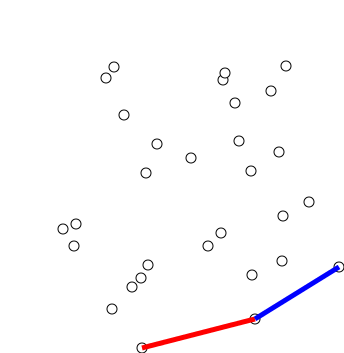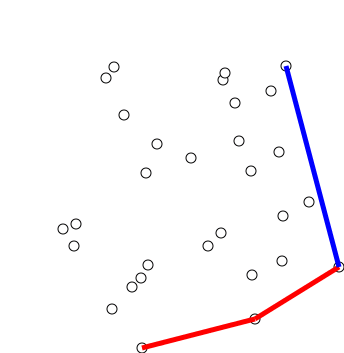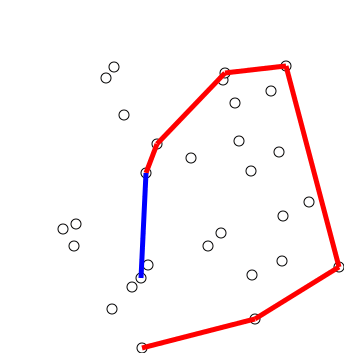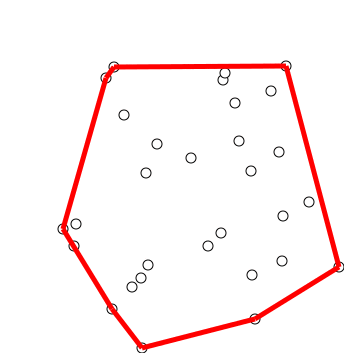
Phase 1 (Sort points): We first find the bottom-most point. The idea is to pre-process points be sorting them with respect to the bottom-most point. Once the points are sorted, they form a simple closed path (See following diagram).

What should be the sorting criteria? computation of actual angles would be inefficient since trigonometric functions are not simple to evaluate. The idea is to use the orientation to compare angles without actually computing them (See the compare() function below)

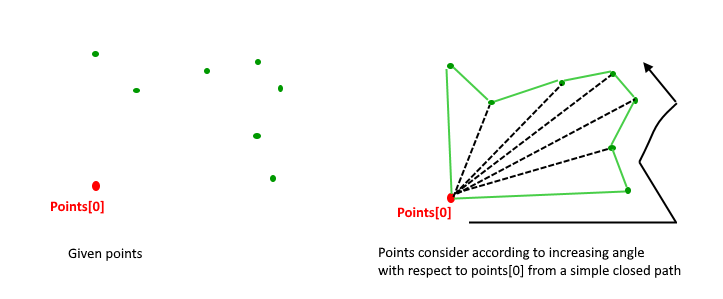
Phase 2 (Accept or Reject Points): Once we have the closed path, the next step is to traverse the path and remove concave points on this path. How to decide which point to remove and which to keep? Again, orientation helps here. The first two points in sorted array are always part of Convex Hull. For remaining points, we keep track of recent three points, and find the angle formed by them. Let the three points be prev(p), curr(c) and next(n). If orientation of these points (considering them in same order) is not counterclockwise, we discard c, otherwise we keep it. Following diagram shows step by step process of this phase

Pseudocode

The Pseudocode of Graham Scan Algorithm is as follows:

let N = number of points
let points[N+1] = the array of points
swap points[1] with the point with the lowest y-coordinate
sort points by polar angle with points[1]
    # We want points[0] to be a sentinel point that will stop the loop.
let points[0] = points[N]
    # M will denote the number of points on the convex hull.
let M = 1
for i = 2 to N:
    # Find next valid point on convex hull.
    while ccw(points[M-1], points[M], points[i]) <= 0:
        if M > 1:
            M -= 1
            continue
        # All points are collinear
        else if i == N:
            break
        else
            i += 1
    # Update M and swap points[i] to the correct place.
    # This code is wrong as explained in the talk page. When M and i are the same,
    the algorithm ends up in an infinite loop.
M += 1
swap points[M] with points[i]

Implementations

Following is the implementation of Graham Scan Algorithm in C++:

• C++

#include <iostream>
#include <stack>
#include <stdlib.h>
using namespace std;
// Part of Cosmos by OpenGenus Foundation
// A C++ program to find convex hull of a set of points. 
struct Point
{
    int x, y;
};
// A globle point needed for  sorting points with reference
// to  the first point Used in compare function of qsort()
Point p0;
// A utility function to find next to top in a stack
Point nextToTop(stack<Point> &S)
{
    Point p = S.top();
    S.pop();
    Point res = S.top();
    S.push(p);
    return res;
}
// A utility function to swap two points
int swap(Point &p1, Point &p2)
{
    Point temp = p1;
    p1 = p2;
    p2 = temp;
}
// A utility function to return square of distance
// between p1 and p2
int distSq(Point p1, Point p2)
{
    return (p1.x - p2.x)*(p1.x - p2.x) +
          (p1.y - p2.y)*(p1.y - p2.y);
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
    int val = (q.y - p.y) * (r.x - q.x) -
              (q.x - p.x) * (r.y - q.y);
    if (val == 0) return 0;  // colinear
    return (val > 0)? 1: 2; // clock or counterclock wise
}
// A function used by library function qsort() to sort an array of
// points with respect to the first point
int compare(const void *vp1, const void *vp2)
{
   Point *p1 = (Point *)vp1;
   Point *p2 = (Point *)vp2;
   // Find orientation
   int o = orientation(p0, *p1, *p2);
   if (o == 0)
     return (distSq(p0, *p2) >= distSq(p0, *p1))? -1 : 1;
   return (o == 2)? -1: 1;
}
// Prints convex hull of a set of n points.
void convexHull(Point points[], int n)
{
   // Find the bottommost point
   int ymin = points[0].y, min = 0;
   for (int i = 1; i < n; i++)
   {
     int y = points[i].y;
     // Pick the bottom-most or chose the left
     // most point in case of tie
     if ((y < ymin) || (ymin == y &&
         points[i].x < points[min].x))
        ymin = points[i].y, min = i;
   }
   // Place the bottom-most point at first position
   swap(points[0], points[min]);
   // Sort n-1 points with respect to the first point.
   // A point p1 comes before p2 in sorted ouput if p2
   // has larger polar angle (in counterclockwise
   // direction) than p1
   p0 = points[0];
   qsort(&points[1], n-1, sizeof(Point), compare);
   // If two or more points make same angle with p0,
   // Remove all but the one that is farthest from p0
   // Remember that, in above sorting, our criteria was
   // to keep the farthest point at the end when more than
   // one points have same angle.
   int m = 1; // Initialize size of modified array
   for (int i=1; i<n; i++)
   {
       // Keep removing i while angle of i and i+1 is same
       // with respect to p0
       while (i < n-1 && orientation(p0, points[i],
                                    points[i+1]) == 0)
          i++; 
       points[m] = points[i];
       m++;  // Update size of modified array
   }
   // If modified array of points has less than 3 points,
   // convex hull is not possible
   if (m < 3) return;
   // Create an empty stack and push first three points
   // to it.
   stack<Point> S;
   S.push(points[0]);
   S.push(points[1]);
   S.push(points[2]);
   // Process remaining n-3 points
   for (int i = 3; i < m; i++)
   {
      // Keep removing top while the angle formed by
      // points next-to-top, top, and points[i] makes
      // a non-left turn
      while (orientation(nextToTop(S), S.top(), points[i]) != 2)
         S.pop();
      S.push(points[i]);
   }
   // Now stack has the output points, print contents of stack
   while (!S.empty())
   {
       Point p = S.top();
       cout << "(" << p.x << ", " << p.y <<")" << endl;
       S.pop();
   }
}
// Driver program to test above functions
int main()
{
    Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
                      {0, 0}, {1, 2}, {3, 1}, {3, 3}};
    int n = sizeof(points)/sizeof(points[0]);
    convexHull(points, n);
    return 0;
}

Complexity

• Worst case time complexity: Θ(N log N)
• Average case time complexity: Θ(N log N)
• Best case time complexity: Θ(N log N)
• Space complexity: Θ(N)

The algorithm takes O(nLogn) time if we use a O(nLogn) sorting algorithm.

The first step (finding the bottom-most point) takes O(n) time. The second step (sorting points) takes O(nLogn) time. Third step takes O(n) time. In third step, every element is pushed and popped at most one time. So the sixth step to process points one by one takes O(n) time, assuming that the stack operations take O(1) time. Overall complexity is O(n) + O(nLogn) + O(n) + O(n) which is O(nLogn)

Applications

The applications of this Divide and Conquer approach towards Convex Hull is as follows:

• Collision avoidance: If the convex hull of a car avoids collision with obstacles then so does the car. Since the computation of paths that avoid collision is much easier with a convex car, then it is often used to plan paths.

• Smallest box: The smallest area rectangle that encloses a polygon has at least one side flush with the convex hull of the polygon, and so the hull is computed at the first step of minimum rectangle algorithms. Similarly, finding the smallest three-dimensional box surrounding an object depends on the 3D-convex hull.

• Shape analysis: Shapes may be classified for the purposes of matching by their "convex deficiency trees", structures that depend for their computation on convex hulls.

• Other practical applications are pattern recognition, image processing, statistics, geographic information system, game theory, construction of phase diagrams, and static code analysis by abstract interpretation.

• It also serves as a tool, a building block for a of other computational-geometric algorithms such as the rotating calipers method for computing the width and diameter of a point set.