Find if a given Binary Tree is a Sub-Tree of another Binary Tree

A sub-tree is a tree itself that is the subset of a bigger binary tree. A subtree of a node means that it is the child of that node. In this article, we will find out different ways to find out if a given binary tree is a sub-tree of another binary tree.

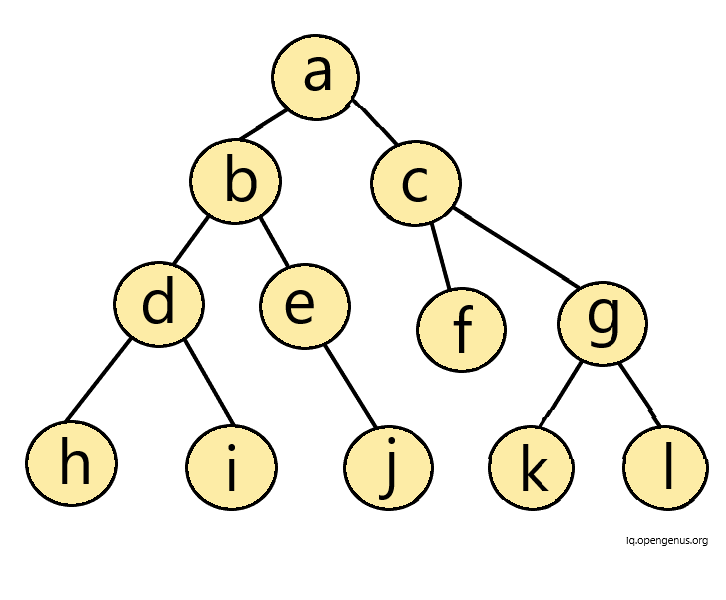
To understand this concept better, let us consider an example of a tree 'Target'.

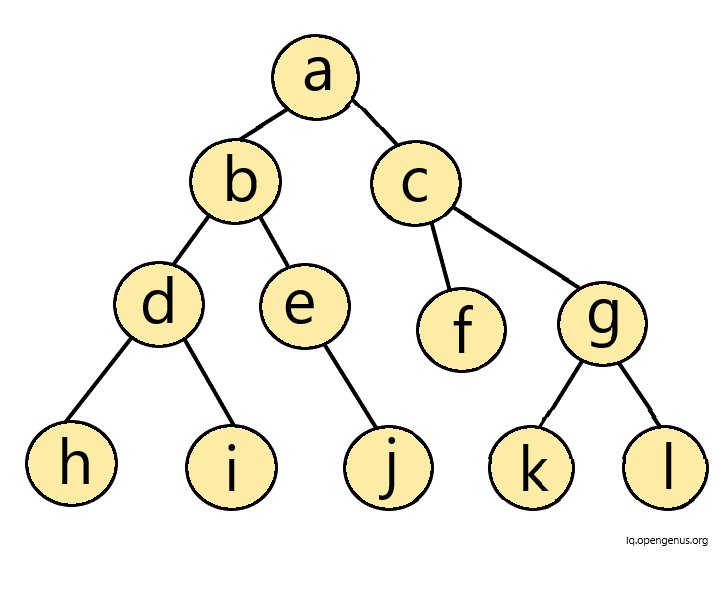
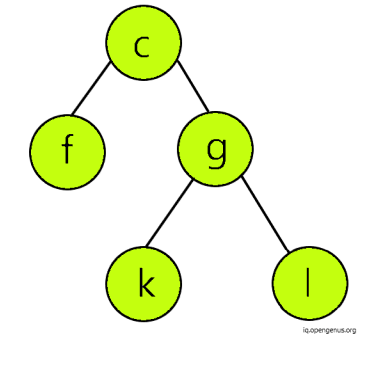
Now, let us consider another tree called 'Source'.

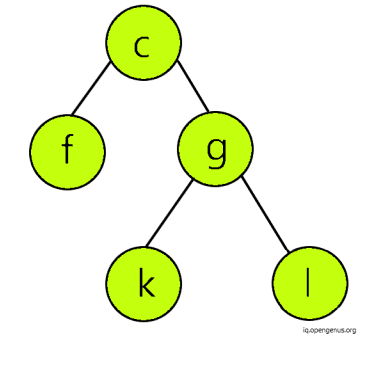
Now, we will start to check from the root node of 'Target', that is 'a'. Since, 'a' is not present in 'Source' tree, then we move on to the the next node in the left subtree.
Upon further iterations, we will get to know that none of the nodes of the 'Source' tree exist in left-subtree of 'Target' tree.
Then, we move on to the right subtree of 'Target' tree. Here, the node 'c' of 'Target' matches the first node of 'Source' tree. Then, we explore the left subtree of the node 'c' of target. Node 'f' also matches the node in 'source' tree. In similar fashion, we iterate and get to know that the entire right-subtree of 'Target' tree matches the 'Source' tree.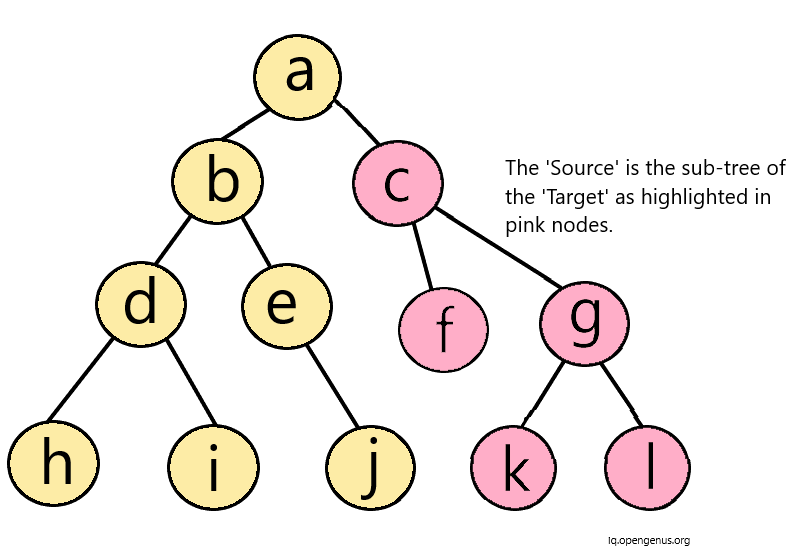

Therefore, 'Source' is the sub-tree of the 'Target' tree.
Hence, in this way we can find out if a tree is the sub-tree of another binary tree.

However, if 'Source' would have been as below, then it wouldn't have been a sub-tree of 'Target' due to the presence of extra 'h' node in the left-subtree of 'f' node.

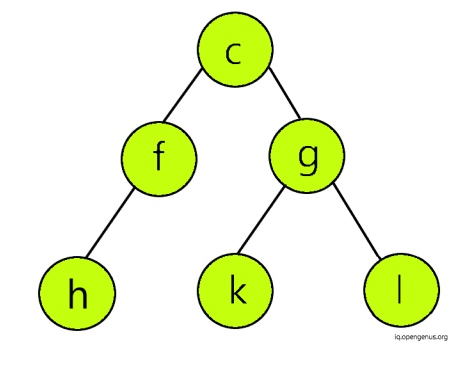
There are different approaches that can be followed to implement this in code.

Approach 1: Recursion

In this approach, we recursively check if the 'Source' exists in the 'Target'.

Algorithm:

Within the function "subtree",
Step 1: If the 'Source' tree is null then return 1
Step 2: If the 'Target' tree is null then return 0
Step 3: If 'Target' and 'Source' are identical then return 1
Step 4: Call function "subtree" by passing arguments- left node of the 'target' tree and the root node of 'source' tree and call function "subtree" by passing arguments - right node of 'target' tree and root node of 'source' tree.
If any of them executes to true, return true.
Here, recursion occurs.

Explaination:

In the above algorithm, we start by creating a function "subtree". In this function, we provide first base condition to return 1 if the 'Source' tree is null. Since, any null tree is a sub-tree of all trees.

Then, we give another base condition if a 'Target' tree is null then no tree can be its sub-tree. Hence, we return 0.

Then, we define third base condition. If the 'Target' tree and 'Source' tree are identical then, we return 1. We check this condition by calling function "identical". This function we check if nodes passed as arguments are both null then return 1.
Else if both are not null then, return true if all of the below 3 conditions are true:

• Data of node of "Target" and "Source" tree are equal.
• Data of left node of "Target" and "Source" tree are equal (via recusion)
• Data of right node of "Target" and "Source" tree are equal (via recusion)

Else, we return false if one node is null and one isn't.

Considering the below mentioned trees,

Tree 'Source':

Tree 'Target':

• In the function "subtree", firsty, neither 'Source' nor 'Target' null. Hence, we check third condition if the two trees are identical.
  We call function "identical".

• Now, we don't enter in its condition 1 since both are not NULL. Following the condition two, we check if 'Source' and 'Target' nodes are equal. Now this condition isn't true for the root node of 'Target' and 'Source' hence we return false. Now the control comes back to "subtree" function.

• Now, we come to the last condition of subtree and recursively call the subtree function again by passing left node and right node of 'Target' respectively along with root node of 'Source'.

• This way upon, recursion we will return true when the right subtree of the 'Target' is executed, since it exactly matches 'Source'.

Let's have a look at the code:

//first, we define the identical function which we will call in "subtree" function

int identical(struct node* a, struct node* b) {

  //if both nodes are null then return true
  
  if (a==NULL && b==NULL) return(true);
  
  // if both are not null then return true if all three mentioned conditions are true
  
  else if (a!=NULL && b!=NULL) {
  
    return((a->data == b->data)&&(identical(a->left, b->left))&&(identical(a->right, b->right)));
  
  }
 
 //if one node is null and one is not null then return false
 
 else return(false);
}

Now, let us define the function "subtree"

int subtree(node* a, node* b){

//if source tree is null then return 1

if(b == NULL){return 1;}

//if target tree is null then return 0

if(a == NULL){return 0;}

// We call identical function here and if a and b are identical then return 1

if(identical(a,b)){
return 1;
}

/* Recurively call subtree function with arguments : 
left node of 'Target' and root node of 'Source' AND 
right node of 'Target' and root node of 'Source'. 
If any of them returns true then the answer returned is true
*/

return(subtree(a->left,b)||subtree(a->right,b));
}

The Time complexity will be O(mn).
The space complexity will be O(n) since the 'n' refers to the number of nodes here.

Approach 2: Pre-Order and In-order Traversal Method

In binary trees, a binary tree can be constructed if a traversals are given. If any one of the traversal method is Inorder then, we can construct the binary tree from given combination of traversals.

To accomplish our task of finding if a tree is a sub-tree of another tree or not, we arrange both 'Target' and 'Source' in preorder and inorder traversals. If the inorder and preorder traversals of 'Source' is substring of inorder and preorder tarversals of 'Target' respectively then the 'Source' is said to be the sub-tree of 'Target'.

The Algorithm is :
Step 1: Find out the preorder and inorder traversals of 'Target' and save them in arrays.
Step 2: Find out the preorder and inorder traversals of 'Source' and save them in arrays.
Step 3: If the arrays of 'Source' are substrings of respective arrays of 'Target' then its a sub-tree else not.

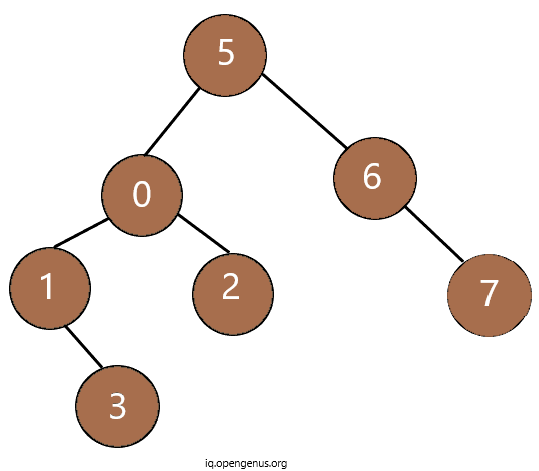
Consider the 'Target' as below:

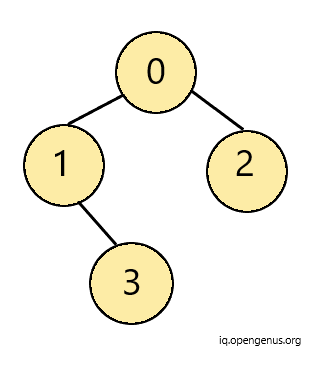
Consider the 'Source' as below:

• The Inorder Traversal of 'Target' is : {1,3,0,2,5,6,7}
• The Inroder Traversal of 'Source' is : {1,3,0,2}
• The Preorder Traversal of 'Target' is : {5,0,1,3,2,6,7}
• The Preorder Traversal of 'Source' is : {0,1,3,2}

Clearly, The arrays of 'Source' are substrings of arrays of 'Target'. Hence, it is a sub-tree.

Now, let's see its implementation in code:

Firstly, we define the fucntion to determine the Inorder Traversal.

/* In this function, we pass the root node of the tree, character array
and i via refernce as it represents the index of array
*/
void Inorder(Node* root, char arr[], int& i)
{

/*If the root is NULL, then we put empty char in array location
and return */

    if (root == NULL) {
        arr[i++] = ' ';
        return;
    }
    /*Else, we recursively call the Inorder Function 
    till all nodes on the left-subtree are traversed*/
    
    Inorder(root->left, arr, i);
    
    // Then, we traverse the root node
    
    arr[i++] = root->key;
    
    // Finally, we traverse the right sub-tree
    
    Inorder(root->right, arr, i);
}

Then, we define the Pre-order Traversal :

/* In the similar fashion as above, we pass the root node,
character array and index of array by reference as arguments
*/
void Preorder(Node* root, char arr[], int& i)
{
// If the root is NULL then we pass empty character to the array
//Then, we return 
    if (root == NULL) {
        arr[i++] = ' ';
        return;
    }
    //Firstly, we traverse the root node
    
    arr[i++] = root->key;
    
    //Then, we traverse the left sub-tree Recursively
    
    Preorder(root->left, arr, i);
    
    //Finally, we recursivelly traverse the right sub-tree
    
    Preorder(root->right, arr, i);
}

Finally, let's implement the function to determine if 'Source' is sub-tree of 'Target' or not

bool isSubtree(Node* Target, Node* Source)
{
    /* Firstly, define the base case :
    - If Source is NULL then return True
    - If Target is NULL then return False
    */
    
    if (Source == NULL)
        return true;
    if (Target == NULL)
        return false;
 
    /*Now, initialise the variables m and n by 0 as they represent 
    the array indexes of 'Target' and 'Source' Traversal arrays
    */
    int i = 0, j = 0;
    
    //declare the arrays
    char inTarget[100], inSource[100];
    
    //Now, call the function Inorder for target and source trees
    Inorder(Target, inTarget, i);
    Inorder(Source, inSource, j);
    
    inTarget[i] = '\0', inSource[j] = '\0';
 
    // If inSource[] is not a substring of inTarget[] then return false
    if (strstr(inTarget, inSource) == NULL)
        return false;
 
    i = 0, j = 0;
    char preTarget[100], preSource[100];
    
    // Calling Preorder Function to store the preorder traversals
    
    Preorder(Target, preTarget, i);
    Preorder(Source, preSource, j);
    
    preTarget[i] = '\0', preSource[j] = '\0';
 
    /* If preSource[] is not a substring of preTarget[], return false
    Else return true*/
    return (strstr(preTarget, preSource) != NULL);
}

This method takes time complexity of O(n) and Space complexity of O(n).

Hence, in this way we can determine if a tree is the sub-tree of another tree via two different approaches.