
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have developed a Python based Web Application using Flask framework to find the prime factorization of any number. The number is provided by the user.
Introduction
I received an email a fews days back with the subject 'The 1 piece of coding advice I wish I had received'. In a nutshell, it stressed out the importance of developers being problem solvers and not developers obsessed with their tools and crippled by the absence of these tools. Languages, frameworks e.t.c are means through which we express our solutions programmatically and are very subjective to a number of factors like the domain, environment, situation and yet the core of software development never changes that is - problem solving.
Honestly, I really wish, I had someone to tell me this before I started writing software. But you know what they say, Better late than never. I started out on that note probably because this article introduces Flask (python micro web framework) through building a prime factorization web application. Abstract away 'Flask' from the topic, and what's left, is integer prime factorization. For what it's worth, this article will be focus more on prime factorization than the flask framework.
Source code
The source code for the application can be downloaded from https://github.com/kiraboibrahim/pollard-rho-prime-factorization
Creating the virtual environment
It has always been good practice to isolate development environments, and pretty sure, I am not quitting today.
Using python venv module
python -m venv flask-sandbox
The above command creates a virtual environment with the name 'flask-sandbox'. This works for python >= 3.3
Using virtualenv
virtualenv --python=/usr/bin/python3 flask-sandbox
Installing flask
source flask-sandbox/bin/activate
flask-sandbox/bin/activate is a relative to wherever you created the virtual environment.
pip install flask
Prime Factorization Algorithm
When a composite is decomposed into a product of smaller integers, that is called integer factorization and if we restrict the factors to be prime factors, then that's called prime
factorization i.e. 864 = 2x2x2x2x2x3x3x3. There is quite a number of prime factorization algorithms i.e. trial division, wheel factorization, Pollard Rho algorithm, Fermat's factorization, special number field sieve e.t.c. We shall use the Pollard Rho algorithm with a flavor of Floyd's cycle detection algorithm - The hare and the tortoise
Pillars of Pollard Rho Algorithm
Birthday Paradox
The birthday paradox answers the question: How many people are need so that the probability of finding at least two people sharing a birthday exceeds 50%? The number of people needed is 23. How? Math ahead!
Let P(A) represent the probability at least two people share the same birthday.
Let P(A') represent the probability that all people in the group have different birthdays
Because events A and A' are mutually exclusive, this yields P(A) = 1 - P(A'). Considering a group of 23 people identified by numbers i.e. 1 referring to person 1, and 2 referring to person 2, and so on. We shall calculate P(A') and then obtain P(A) from the above equation.
Let E1 represent the event of person 1 having a birthday given that the preceding birthdays(for person 1, no one precedes him) has been taken, E2 represent the event of person 2 having a birthday given the preceding birthdays(person 1 BD) have been taken, and so on till E23.
P(E1) = 365/365, P(E2) = 364/365, P(E3) = 363/365, P(E4) = 362/365, ..., P(E23) = 343/365
We are using conditional probability to compute the above probabilities. Let's take an example of the computation of P(E2)
Remember E2 is the event of person 2 having a birthday given the birthday of person 1 has been taken, thus n(E2) = 364 and n(S) = 365, hence P(E2) = n(E2)/n(S) = 364/365
Computing P(A')
P(A') = P(E1) x P(E2) x P(E3) x P(E4) x ... x P(E23)
P(A') = 365/365 x 364/365 x 363/365 x ... x 343/365
P(A') = 0.4927 (approx.)
P(A) = 1 - 0.4927 = 0.5073
A probability of 0.5073 shows that if we have at least a group of 23 people, we are 50% likely to have birthday collisions. Despite a large sample space size of 365, we only needed a small number of people(23) to be 50% certain that we have atleast two people sharing birthdays - This is why it's referred to as a paradox.
From the above, we deduce that, because 23 < sqrt(365), for any set of size N, we only need group of size k = sqrt(N) to start having collisions - repetitions in a sequence.
Floyd's Cycle Detection Algorithm
Floyd's cycle detection algorithm uses two pointers - the Hare and the Tortoise. The hare pointer moves faster (i.e. twice as fast) than the tortoise pointer. The essence of the algorithm is, if in any way, a sequence exhibits a cyclic characteristic, we are certain, the hare pointer will overlap the tortoise pointer and in that case, a cycle exists.
Imagine two runners on a circular track, one running faster than the other, we are very much certain for the faster runner overlap the slow runner simply because it is a circular track as opposed to the case if it were a straight track. In which case, the faster runner willnot overlap the slow runner.
Pollard Rho Algorithm
This algorithm factors a number say N, into its factors i.e N = PxQ.
The brute force approach would be trial division - Testing division with all prime numbers less than N, but this approach becomes inefficient with large inputs. Pollard Rho is a probabilistic algorithm that improves the chances of finding the factors of N. It uses a polynomial pseudo random function of the form x2 + a (mod N), where a is the seed, to generate a set random numbers { x1, x2 , ..., xk } - where k is the size of the set. The size of k is sqrt(N).
Each element in the sequence generated is computed from the preceding element i.e x2= f(x1), x3 = f(x2) and so on where f(x) is a PRF(Pseudo Random Function). The only exceptional element in the sequence is x1(the starting element) which is just chosen, say 2.
After generating the random sequence, we do pairwise differences i.e. xi - xj, and then test GCD(|xi - xj|, N) > 1. If the preceding condition is met, it implies we found a non trivial factor of N which is (|xi - xj|). If one of the factors of N, say P has been found, therefore the other factor Q = N/P.
After finding the two factors P and Q, we recursively factorize those factors until we are only left with prime factors.
The PRF f(x) generates a finite sequence and thus, the sequence will eventually repeat or cycle. As the birthday paradox suggests, the number of xk required for repetitions to starting occuring is sqrt(N). To combat the cycling, we use the Floyd cycle detection algorithm and after detecting the cycle, we change the value of a, which is known as the seed.
Why (xi - xj) and not just xi only
Imagine given a set S of numbers from 1 to 1000. What are chances that we land on a number 20. The answer is 1/1000 since each number in S is equally likely. Suppose we are allowed to randomly pick two numbers - xi, xj (xi and xj can be the same) from set S, what are the odds that xi - xj = 20?. The answer is (980 * 2)/(1000 * 1000) = 29 / 25000. With no doubt, our odds have improved. Therefore, we do pairwise differences to improve our chances of landing on the factor of N. Always remember that Pollard Rho algorighm is a probabilistic algorithm.
Implementation of Pollard Rho Algorithm
The source code for all the functions discussed here resides in the prime_factorization.py file. Download the source code and follow along.
def gcd(a: int, b: int) -> int:
if a == 0:
return b
if b == 0:
return a
return gcd(b, a % b)
def f(a: int, n: int, seed: int):
return ((a * a) - seed) % n
def factorize(n: int):
x = y = 2
d = 1 # If the gcd is 1, then (x-y) and n are coprime
seed = random.randint(2, n - 1)
while d == 1 or d == n:
x = f(x, n, seed)
y = f(f(y, n, seed), n, seed) # Move y twice as fast as x
d = gcd(abs(x - y), n)
if y == x: # The function f() produces a cyclic sequence, a loop occurs if y overlaps x
x = y = 2
seed = random.randint(2, n - 1)
return d
def is_prime(n: int) -> bool:
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
return True
def prime_factorize(n: int) -> list[int]:
if is_prime(n):
return [n]
elif n % 2 == 0:
# Exhaust prime factors of 2 because the random seq generators tends to produce odd values
return [2] + prime_factorize(n // 2)
else:
first_factor: int = factorize(n)
second_factor: int = n // first_factor
return sorted(prime_factorize(first_factor) + prime_factorize(second_factor))
Explanation
- gcd(a, b) - Finds the largest integer that divides both a and b with the remainder being zero.
- f(a, n, seed) - This is the pseudo random function that generates the pseudo random sequence.
- factorize(n) - Finds the factors(not necessarily prime) of n, using the Pollard Rho algorithm.
- is_prime(n) - Checks if n is prime.
- prime_factorize(n) - The integral part of our application, that ties all the above functions together.
factorize(n)
def factorize(n: int):
x = y = 2
d = 1 # If the gcd is 1, then (x-y) and n are coprime
seed = random.randint(2, n - 1)
while d == 1 or d == n:
x = f(x, n, seed)
y = f(f(y, n, seed), n, seed) # Move y twice as fast as x
d = gcd(abs(x - y), n)
if y == x: # The function f() produces a cyclic sequence, a loop occurs if y overlaps x
x = y = 2
seed = random.randint(2, n - 1)
return d
This function finds a non trivial factor of a number n by using the Pollard Rho algorithm as explained above. The local varible x can be considered the tortoise and the local variable y can be considered the hare as per the Floyd cycle detection algorithm. Both x and y are initialized to the value 2.
The local varible d is the greatest common denominator (GCD) and its initialized to 1 because if if the GCD(a,b) = 1, this implies the numbers a and b are coprime and no suprise, this condition holds true for the whole iteration in the receding while loop.
The seed is randomly generated with in a range of 2 and n-1 inclusive. The while loop runs for as long as the the GCD(|x-y|, n) == 1 || GCD(|x-y|, n) == n. With in the while loop, we check for any cycles i.e. y == x, and in that case, x and y are reinitialized to 2 and the seed is also changed to try another sequence.
Something worthy noting is how x and y are computed i.e. x = f(x, n, seed) and y = f(f(y, n, seed)) where f is the pseudo random fuction. y is moving twice fast because the pseudo random function is invoked twice. This implies y will always be two 'steps' ahead of x.
prime_factorize(n)
def prime_factorize(n: int) -> list[int]:
if is_prime(n):
return [n]
elif n % 2 == 0:
# Exhaust prime factors of 2 because the random seq generators tends to produce odd values
return [2] + prime_factorize(n // 2)
else:
first_factor: int = factorize(n)
second_factor: int = n // first_factor
return sorted(prime_factorize(first_factor) + prime_factorize(second_factor))
This is the integral component of the application. It recursively prime factorizes the factors of n. i.e if N = P x Q, then this function goes ahead to recursively prime factorize P and Q and so on and so forth.
One peculiar and obscure block of code in this function is the elif n%2==0 block that keeps finding the prime factors of 2 for as long as they exist. It isn't coincedental this wasn't covered in the Pollard Rho explanation above. A greater percentage of the Pollard Rho algorithm pseudo code(even the one I read) will not contain that block. So how does it come to have a spot in my Pollard Rho algorithm implementation?
This hack is attributed to the answer given by Tengu on this math.stackexchange.com question which pertains to how Pollard Rho algorithm fails to factorize some numbers. Having faced issues(infinite loops) with some numbers like 8 during testing, I relentlessly scoured the internet for some answers and fruitfully, I found one(the one above)
In short, the problem was caused by the difference in parity of *f(x) and f(f(x)) and thus the difference - f(x) - f(f(x)) was always odd, and for those numbers that had a prime factor of 2(the only even prime factor), the factorize() function infinitely looped. Well, Tengu's answer suggested using a different pseudo random function - f(x) = x2 + 2 (mod N) or exhausting prime factors of 2 before applying Pollard Rho algorithm -factorize(). I chose the latter for its simplicity(atleast for me).
The Flask Application
Structure
pollard-rho-prime-factorization/
├─ templates/
│ ├─ index.html
├─ __init__.py
├─ app.py
├─ prime_factorization.py
app.py
from flask import Flask
from flask import render_template
from .prime_factorization import prime_factorize
app = Flask(__name__)
@app.route("/factorize")
def index():
return render_template("index.html")
@app.route("/factorize/<int:number>")
def prime_factorize_(number):
prime_factors = prime_factorize(number)
return render_template("index.html", **{'number': number, "result": prime_factors})
if __name__ == "__main__":
app.run(debug=True)
At the top of the file, we import the Flask class, render_template function, and lastly the prime_factorize function.
We then instantiate the WSGI application object from the Flask class. At instantiation, we pass module name of the app.py as the first argument which in our case points to pollard-rho-prime-factorization.app. Flask uses this argument for finding resources like templates e.t.c and most importantly, extensions rely on this to provide very insightful debugging information.
We then define two routes i.e. factorize/ and factorize<int:number> and associate them with functions(views) that will be invoked when the respective routes are visited. Associating routes to views in Flask is quite succint with the use of the route decorator defined in the Flask class.
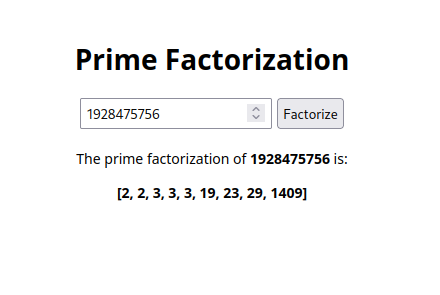
- factorize/ - This route's view function renders the prime factorization form which prompts for the number to prime factorize.
- factorize/<int:number> - This route's view function finds the prime factors that constitute the number passed in the number argument. The render_template function is passed keyword arguments that represent the variables that are needed in the template - index.html. In our case, we pass the number that has been factored and the constituent prime factors of the number.
Template
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Prime Factorization {% if number %} Of {{ number }} {% endif %}</title>
<!-- Albert Sans Google Font -->
<link rel="preconnect" href="https://fonts.googleapis.com">
<link rel="preconnect" href="https://fonts.gstatic.com" crossorigin>
<link href="https://fonts.googleapis.com/css2?family=Albert+Sans&display=swap" rel="stylesheet">
<style>
body {
font-family: 'Albert Sans', sans-serif;
font-size: 14px;
}
.container {
max-width: 500px;
padding: 1rem;
}
.find-prime-factors-form__number {
padding: 5px;
margin-right: 5px;
}
.prime-factors-result {
margin-top: 20px;
}
.flex-column {
flex-direction: column;
}
.d-flex {
display: flex;
}
.align-items-center {
align-items: center;
}
.justify-content-center {
justify-content: center;
}
.text-center {
text-align: center;
}
</style>
</head>
<body class="d-flex flex-column align-items-center">
<div class="container">
<h1>Prime Factorization</h1>
<form class="find-prime-factors-form d-flex justify-content-center">
<input class="find-prime-factors-form__number" type="number" placeholder="Input number to factorize"
required="required" {% if number %} value="{{ number }}" {% endif %}>
<button class="find-prime-factors-form__submit" type="submit">Factorize</button>
</form>
{% if result %}
<div class="prime-factors-result">
<p class="text-center">The prime factorization of <strong>{{ number }}</strong> is:</p>
<p class="text-center">
<strong>{{ result }}</strong>
</p>
</div>
{% endif %}
</div>
<script>
let prime_factors_query_form = document.getElementsByClassName("find-prime-factors-form")[0];
let number_to_factorize_input = document.getElementsByClassName("find-prime-factors-form__number")[0];
prime_factors_query_form.onsubmit = (event) => {
event.preventDefault();
const number_to_factorize = number_to_factorize_input.value;
document.location = `/factorize/${number_to_factorize}`;
}
</script>
</body>
</html>
The same template(index.html) is used to query for the number to factorize and to render the result. With in the template, we initialize the value of the input field if the variable number is defined in the template context(variables passed to the template during rendering). If the result has also been passed in the template context, the result of prime factorization is rendered in a div.
Conclusion
We as developers should spend more time on honing our problem solving skills. We are always employed to solve problems. However, one shouldn't belittle the importance of tools, frameworks, programming languages e.t.c, they have always been around and they aren't going anyway. Learn and practice problem in them.
