Mathematical Programming is used to find the best or optimal solution to a problem that requires a decision or set of decisions about how best to use a set of limited resources to achieve a state goal of objectives.

Linear programming requires that all the mathematical functions in the model be linear functions. We have solved linear programming problems in Python using cvxpy library.

Learn how to formulate Linear Programming problems

Mathematical formulation

Decision variables: X₁, X₂, X₃, .... X_n
Objective function or linear function: Z

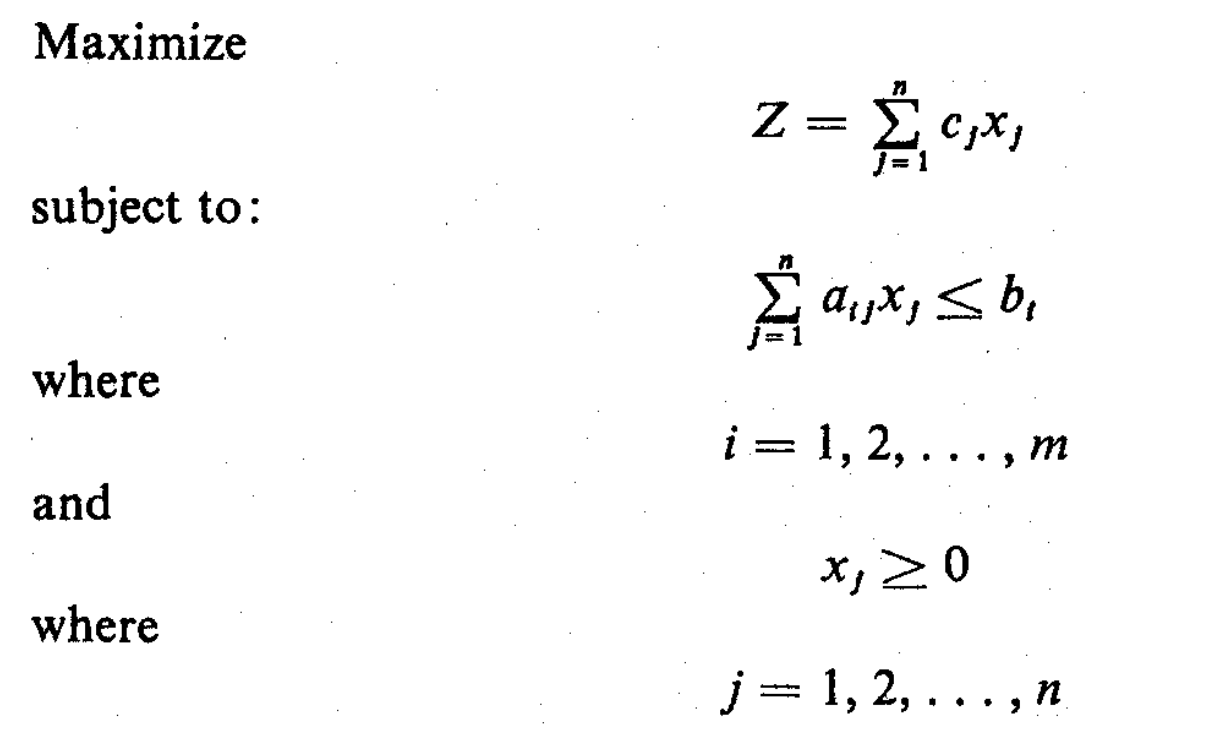
Library used

Here, we use the library, cvxpy to find the solution of the linear programming problem(lpp).

To install this library, use the following command:

pip3 install cvxpy

To include it in our code, use

import cvxpy as cp
import numpy as np

EXAMPLE 1

Problem

Here, we solve the following LPP:

Maximise: z = x₁ + x₂

Subject to

• 4 x₁ + 3 x₂ <= 12
• -3 x₁ + 4 x₂ <= 12
• 0 <= x₁, x₂ <= 2

The expected solution is

• z = 3.5
• x₁ = 1.5
• x₂ = 2

CODE

Step 1: First define the number of variables that would be used

For example, if only two x_is would be used,

x = cp.Variable(shape=(2,1), name="x")

This line creates a column matrix of dimensions 2 x 1 (in a general case, if n is the number of linear programming variables, then a column matrix of dimensions n x 1 should be made.)

Step 2: Define the constraints

Here the constraints are as follows

x1	x2	Inequality	Constraint
4	3	<=	12
-3	4	<=	12

All values of x lie between 0 and 2 both inclusive.

A = np.array([[4,3],[-3,4]])
constraints = [cp.matmul(A, x) <= 12, x<=2, x>=0]

The above lines first make a 2 x 2 matrix (as described in the table above). Since both of their constraints are the same, we can define the constraint in a single line, by making the matrix <= 12.

Multiple constraints on both the variables can be defined using x as a general variable.

For defining multiple single lined distinct constraints, use the following format:

A x <= B

Where <= can be replaced by any other inequality symbol.

Here A is a square matrix of dimensions n x n where n is the number of varibles in the linear programming problem, x is as defined in the previous step, and B is a column matrix of dimensions n x 1.

For example, for defining the following constraints, use the following snippet: (n = 3)

x1	x2	x3	Inequality	Constraint
4	3	2	<=	12
-3	4	2	<=	-10
-2	3	1	<=	14

A = np.array([[4,3,2],[-3,4,2],[-2,3,1]])
B = np.array([[12],[-10],[14]])

constraints = [cp.matmul(A, x) <= B, x<=2, x>=0]

Step 3: Define the objective function

Here the objective function is z = x₁ + x₂

objective = cp.Maximize(cp.sum(x, axis=0))

For an objective function z = 3 x₁ + 4 x₂, define a new 1 dimensional array containing the different parameters in the objective function as follows:

r = np.array([3,4])
objective = cp.Maximize(cp.matmul(r, x))

Step 4: Define the problem and then solve it

The problem is defined by the objective function and the constraints.

problem = cp.Problem(objective, constraints)
solution = problem.solve()

Step 5: Print the maximised objective funstion, and the x values

print(solution)
print(x.value)

Here, solution contains the value of the objective function, and x.value is the column matrix, containing the values of x_i.

Final code

import cvxpy as cp
import numpy as np

x = cp.Variable(shape=(2,1), name="x")
A = np.array([[4,3],[-3,4]])

constraints = [cp.matmul(A, x) <= 12, x<=2, x>=0]
objective = cp.Maximize(cp.sum(x, axis=0))
problem = cp.Problem(objective, constraints)

solution = problem.solve()
print(solution)
print(x.value)

Output of the code

3.4999999999296327
[[1.5]
 [2. ]]

Here the first line denotes the solution while the next two lines denote the values of the two parameters.

EXAMPLE 2

Problem

Here, we solve the following LPP:

Minimize: z = 4 x₁ + 2 x₂

Subject to

• 4 x₁ + 3 x₂ <= 12
• -3 x₁ + 6 x₂ <= 10
• x₁ >= 1
• 0 <= x₁, x₂ <= 5

The expected solution is

• z = 4.00
• x₁ = 1.00
• x₂ = 0.00

Code

import cvxpy as cp
import numpy as np

x = cp.Variable(shape=(2,1), name="x")

A1 = np.array([[4,3],[-3,6]])
A2 = np.array([1,0])

B = np.array([[12],[10]])

constraints = [cp.matmul(A1, x) <= B, cp.matmul(A2, x) >= 1, x<=5, x>=0]

r = np.array([4,2])
objective = cp.Minimize(cp.matmul(r, x))

problem = cp.Problem(objective, constraints)

solution = problem.solve()
print(solution)
print(x.value)

Output of the code

3.9999999998494915
[[1.0000000e+00]
 [7.7046817e-11]]

With this article at OpenGenus, you must have the complete idea of solving Linear Programming problems in Python. Enjoy.