Spell Checker in C

In this article, we have developed a Spell Checker tool in C Programming Language. It takes a string as input, highlight the words with wrong spelling and makes possible suggestions for each wrong word.

Softwares which fixes our lines have made our lives a lot easier right? These kinds of softwares have been used in numerous places like Google docs, Word, search engines, keyboards and after the introduction of Grammarly we can see it in every possible data entry fields on the web. It's safe to say that everyone has used this type of software in some form or another.

Here I have built a spell-checker program to demonstrate how it works.

Table of Contents
We can split the entire concept into two parts. To see the code which I am explaining here click here.

• Features & Requirements
• Why Trie?
• Spelling Error Detection
• Spelling Correction
• Output
• Conclusion

Features & Requirements

The feature of this program would be to take a string input from the user and highlight the wrong words in it (if any). Then it would list out the wrong words along with the suggested right words.

For this program to work we need the following:

• A large and accurate dictionary of correctly spelled words. You can use the one in the repo else find a new one.
• A technique to check the accuracy of a particular word.
• An algorithm to suggest correct words and also understand its working, here I have used Levenshtein distance algorithm.
• A strong understanding o Trie data structure.
• A firm grasp on C programming.

Why Trie?

Trie is a tree-based data structure that is often used for efficient retrieval of a key in a large dataset of strings. In the case of a spell-checker, a Trie is used to store a dictionary of words, and the spell-checker can quickly check if a given word is present in the dictionary by traversing the Trie. The advantage of using a Trie over other methods is that it has a faster time complexity for searching, insertion, and deletion operations. Other methods such as hash tables or binary search trees can also be used for this purpose, but a Trie is considered more efficient for large datasets of strings. Another advantage is that Trie is space efficient, which is a big plus when the dictionary is very large, as it can save memory. A Trie, also known as a prefix tree, is a data structure that can be used to efficiently store and search for words in a large dictionary.

Another advantage of using a Trie over other data structures such as a hash table or a binary search tree is that it allows for efficient prefix matching. This means that as the user types in a word, the spell-checker can quickly suggest words that start with the same letters as the user's input. This can improve the user experience by reducing the number of transformation distance, needed to find the correct word.

In addition to Trie, other methods like Aho-Corasick algorithm, BK-tree, and others are used in spell checkers but Trie is the most efficient one among them.

Spelling Error Detection

So to check if a particular word is right or wrong, we need a reference, for that I took the Ofxord 3000 dictionary. It dosen't have all the words but we can use that for the time being.

To determine the accuracy of the word, here we will be using one of the popular data structure known as Trie data structure.

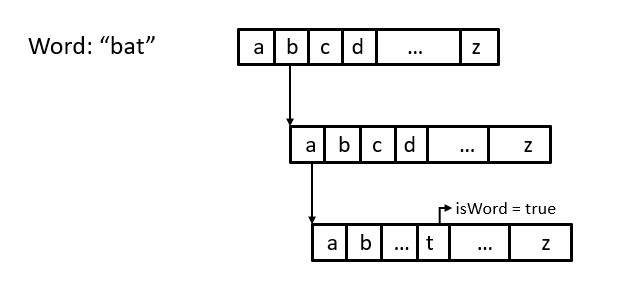
Here in my program I have first stored all the words in the dictionary.txt using a Trie using the loadDictionary() code. For these purpose we need a Trie node with a boolean variable isWord initialized to be false, to verify the presence of a word, 26 key so that each of these keys will point to a node with 26 keys and it will go on like that. So lets imagine there is a word "bat", to store it we will first go to the root node and then find "b" in it, which would be the second node. Then we would go to the node pointed by the "b" key of the root node. Once we reach the child node of "b" key we will find "a" which is the first key in that node then we will go to the node pointed by "a" and then we will find "t" in the child node, which happens to be the 19th key in the node. After we find the "t" key we would turn the isWord variable of that key to true to indicate that a word is formed there. The following code demonstrates it.

typedef struct node
{
    bool isWord;
    struct node *children[N];
} node;

The loadDictionary() is as follows. This function opens the dictionary.txt file and takes each of those words and stores in the Trie. The function first allocates the required memory using malloc() and points their children to NULL.Then it opens the file and takes each word then create a loop and then take each letter and points it accordingly. Here, we calculate the position value of a particular letter using idx = (int)word[i] - (int)'a';, then we create a child node for that key by allocating memory for it, then point all the key of that child node to NULL then move forward until you reach the last letter of the word. At this time you are at the last key of that word, now you will assign this key as true, which indicates that a word exists there.

bool loadDictionary()
{
    root = malloc(sizeof(node));
    if (root == NULL)
    {
        return false;
    }
    root->isWord = false;
    for (int i = 0; i < N; i++)
    {
        root->children[i] = NULL;
    }

    FILE *file = fopen("dictionary.txt", "r");
    if (file == NULL)
    {
        unload();
        return false;
    }

    int idx;
    char word[46 + 1];

    while (fscanf(file, "%s", word) != EOF)
    {
        node *child = root;

        for (int i = 0, l = strlen(word); i < l; i++)
        {
            idx = (int)word[i] - (int)'a';

            if (child->children[idx] == NULL)
            {
                child->children[idx] = malloc(sizeof(node));
                if (child->children[idx] == NULL)
                {
                    return false;
                }
                child->children[idx]->isWord = false;
                for (int j = 0; j < N; j++)
                {
                    child->children[idx]->children[j] = NULL;
                }
            }
            child = child->children[idx];
        }
        child->isWord = true;
        _size++;
    }
    fclose(file);
    return true;
}

The following represents how it would look.

Like this every word would be stored in the Trie data structure. Now after storing all the words in the Trie data structure, we will accept the input from the user.

After getting the input we will iterate through the string and pass each of those words in the string to a function called check() which will return true if a particular word exists like that in the dictionary else it would return false.

So how does it confirm if a word exists or not. Its quite easy, check() would do that for us. We would iterate through the Trie data structure according to the letters in the word. We would return false if there are no children for a particular key and there are letters remaining in the word. Once we reach the last letter (so we would have reached the corresponding node) we would just return isWord which is a boolean value and this would check if a value is correct or wrong! The following code represents it.

bool check(const char *word)
{
    int idx;
    node *child = root;

    for (int i = 0, l = strlen(word); i < l; i++)
    {
        idx = (int)tolower(word[i]) - (int)'a';

        child = child->children[idx];
        if (child == NULL)
        {
            return false;
        }
    }
    return child->isWord;
}

Now our correction process is over now lets see how do we do the suggestion work.

Suggestion

To come out with suggestion here I have used Levenshtein distance algorithm. It is an algorithm which is also known as edit distance algorithm. It is a way to measure the similarity between two strings. The algorithm calculates the minimum number of single character edits like insertion, deletions or replacements needed to change one string to another.

In my program I have used suggest() function which uses the Levenshtein distance algorithm to find the words in the dictionary that are the closest match to the misspelled word. The function first compares the misspelled word to each word in the dictionary using the Trie data structure and calculates the Levenshtein distance between them. The words with the smallest distance are considered to be the closest match and are returned as suggestions.

The Levenshtein distance algorithm is implemented using dynamic programming techniques. The function creates a 2-D array dp[n+1][m+1] where n is the length of the misspelled word and m is the length of the word from the dictionary. The algorithm then fills this array with the Levenshtein distances between the substrings of the two words. The value in the array dp[i][j] represents the Levenshtein distance between the first i characters of the misspelled word and the first j characters of the word from the dictionary. The final value in the array dp[n][m] is the Levenshtein distance between the two words.

The int dp[MAX_LENGTH + 1][MAX_LENGTH + 1]; matrix for transforming from one word to another:

The above matrix is formed with the help of levenshtein_distance() to which we pass two words. One would be the wrong word and the other would be the word from dictionary. With this algorithm, the function returns the transformation distance from one word to the other. If the distance is below 3 we put the word to the suggestions[] array. When the size of the array reaches MAX_SUGGESTIONS we break from the loop and closes the dictionary.txt file and return the array. The below function demonstrates the same.

int suggest(const char *word, char suggestions[MAX_SUGGESTIONS][MAX_LENGTH + 1])
{
    int num_suggestions = 0;
    int min_distance = INT_MAX;

    // Open dictionary file
    FILE *file = fopen("dictionary.txt", "r");
    if (file == NULL)
    {
        printf("Error");
        return 0;
    }

    // Read words from dictionary and calculate Levenshtein distance
    char dict_word[MAX_LENGTH + 1];
    while (fscanf(file, "%s", dict_word) != EOF)
    {
        int distance = levenshtein_distance(word, dict_word);
        if (distance < min_distance && distance < 3)
        {
            num_suggestions = 0;
            strcpy(suggestions[num_suggestions], dict_word);
            num_suggestions++;
            min_distance = distance;
        }
        else if (distance == min_distance && distance < 3)
        {
            strcpy(suggestions[num_suggestions], dict_word);
            num_suggestions++;
        }
        if (num_suggestions == MAX_SUGGESTIONS)
        {
            break;
        }
    }

    fclose(file);
    return num_suggestions;
}

For each of the misspelled word after getting the suggestion array, we form it in the form of a 3-D matrix char display_suggest[MAX_INCRT_WORDS][MAX_SUGGESTIONS + 1][MAX_LENGTH];. Where the first element in each row is a wrong word and the ones following it are the suggestions for that word. The following code demonstrates it.

if (!check(word))
            {
                printf("\033[1;31m%s\033[0m ", word);
                strcpy(display_suggest[incrt_words][0], word);
                char suggestions[MAX_SUGGESTIONS][MAX_LENGTH + 1];
                int num_suggestions = suggest(word, suggestions);
                if (num_suggestions > 0)
                {
                    for (int i = 0; i < num_suggestions; i++)
                    {
                        strcpy(display_suggest[incrt_words][i + 1], suggestions[i]);
                    }
                }
                incrt_words++;
                printf("%s", " ");
            }

Now lets move on to the output for the program.

Output

Conclusion

The above mentioned approach is a method to suggest correct words using Trie and Levenshtein distance, which is a simple and an efficient approach, but it may not always present correct answer. This is because the method is purely based on the exact match of words and the similarity between the misspelled word and the words in the dictionary. However, this method does not take into account the context of the sentence or the grammatical structure of the language. There are several scenarios where this method may fail. This is the reason why big companies who uses these features integrate Natural Language Processing (NLP) into it. NLP techniques like machine learning, deep learning and neural networks can be used to train a spell-checker on a larger dataset of text. With these techniques, the spell checker would be able to identify patterns and features in the text given to it and this can help to improve the accuracy of the spell checker and make it more robust to different types of errors.

In short, we can say that the implementation using Trie and Levenshtein distance method is simple and efficient, but may not provide the accuracy we wish for. Natural Language Processing (NLP) techniques can be used to improve the accuracy of the spell checker by taking into account the context and grammar of the text.

So by the end of this article at OpenGenus, I am hoping that you have understood the concept of spell checking and its implementation.