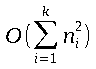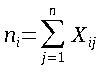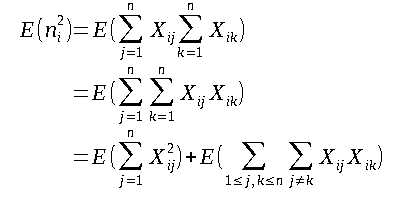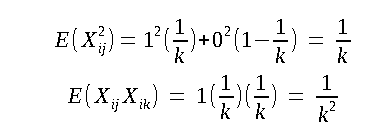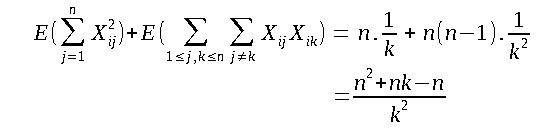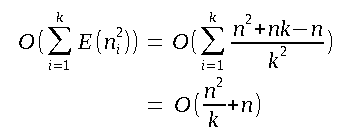Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained the Time and Space Complexity analysis of Bucket sort along with its algorithm, space complexity and time complexity for worst case, average case and best case.
Table of Contents
- Introduction to Bucket Sort
- Algorithm
- Time complexity analysis
- Worst case time complexity
- Average case time complexity
- Best case time complexity
- Space complexity
- Comparison with other sorting algorithms
In short,
- Time complexity:
O(n + k) - Space Complexity:
O(n + k) - Worst case:
O(n²) - Best Case:
O(n + k) - Average Case:
O(n + n²/k + k),O(n)when k = Θ(n)
where
- n is the number of elements
- k is the number of buckets
Introduction to Bucket Sort
Bucket Sort is a type of sorting algorithm in which the individual elements of the input array are distributed into several groups which are known as buckets. One bucket is capable of holding more than one element simultaneously. Each bucket is then sorted individually, either by making use of some other sorting algorithm, or by recursively applying the same bucket sorting algorithm.
Finally, when each bucket has been sorted, they are then combined to form the final and complete sorted array.
Bucket Sort is a stable sorting algorithm.
Algorithm
Bucket sort is especially useful when we are dealing with floating-point values.
Here is the algorithm for bucket sort:
define function bucketSort(arr[]) as
step 1: create as many empty buckets (lists or arrays) as the length of the input array
step 2: store the array elements into the buckets based on their values (described in step 3)
step 3: for i from 0 to length of arr do
(a) bucket_index = int((n * arr[i]) / 10) //here n is the length of the input array
(b) store the element arr[i] at bucket[bucket_index]
step 4: for i from 0 to length of bucket do:
(a) sort the elements stored inside bucket[i], either by applying recursion or by
some other sorting method
step 5: push the values stored in each bucket starting from lowest index to highest index to a
new array/list
step 6: return the sorted array/list
Now let us understand as to how this algorithm works with the help of an example.
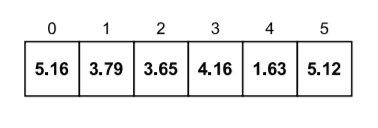
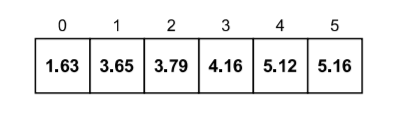
Suppose we want to sort the following array by using Bucket Sort.
Let's follow the algorithm now to sort the array through Bucket Sort.
- The size of the input array is 6, so we have to create 6 (k = 6) empty buckets.
- Now let's start inserting the elements from the input array into the bucket by following the algorithm.
- Following step 3 from the algorithm, when i = 0, we get
bucket_index = int((6 * 5.16) / 10)
= int(30.96 / 10)
= int(3.096)
= 3
Therefore, the element present at arr[0], which is 5.16, will be inserted to the bucket at index 3.
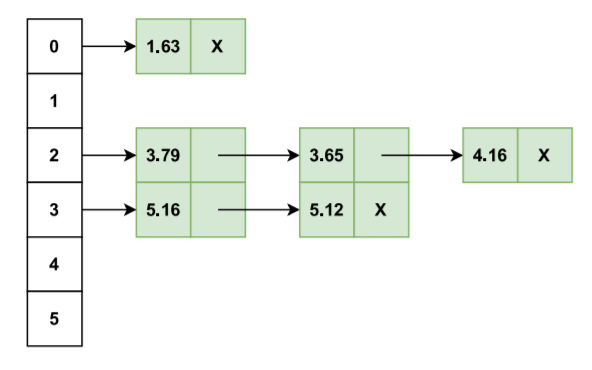
Following this step for each element, we will get our final bucket list as follows:
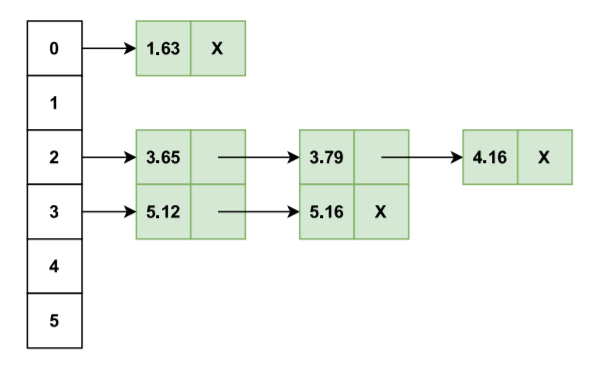
- Moving onto step 4, we have to sort the elements stored inside each bucket individually either by recursion or by some other sorting algorithm, and then combine the buckets to get our final sorted array. For our example and for the purpose of analysis, let us use the Bubble sort algorithm to sort each bucket (refer to this article for the Bubble sort algorithm). After the sorting of each individual bucket, we will have the following final bucket structure:
- Do you notice something in the final figure?
When you move down in the bucket list from the first index (0) to the last index (5), you will notice that we already have our complete sorted array there. We just simply have to extract it from the bucket list in a similar manner.
-
Since the all the buckets have been sorted individually, we can extract the sorted array/list from the final bucket structure.
-
We will start pushing the elements stored in the bucket list, starting from the first index (0) to the last index (5) to a new array/list. This operation will result in a sorted array.
-
Final array obtained is:
Time complexity analysis
The time complexity in Bucket Sort largely depends upon the size of the bucket list and also the range over which the elements in the array/list have been distributed. For example, if the elements in the array don't have a significant mathematical difference between them, it could result in most of the elements being stored in the same bucket, which would significantly increase the complexity of the algorithm.
Consider the following snippet from the algorithm (step 5):
for each bucket b in bucket_list do
for each element i in b do
push i to array
Let us suppose that there are a total of k different buckets, so the outermost loop will take at least O(k) time.
The inner loop will take at least O(n) time overall, since there are a total of n elements distributed across the bucket list.
Hence, we can conclude that the overall complexity of the Bucket Sort will be O(n + k).
Question
The worst case time complexity of Bucket Sort (for our example) should be?
Worst case time complexity
As mentioned earlier, if the elements in the array don't have a significant mathematical difference between them, it could result in most of the elements being stored in the same bucket, which would significantly increase the complexity of the algorithm.
The scenario when every element is stored in the same bucket is when the worst case in terms of time complexity actually happens.
In our case, since we are using the Bubble sort algorithm to sort each bucket, the worst case would occur when we have to first loop over n items in the input array (to store them in the bucket list) and since all of them will be stored inside the same bucket, the worst case of the Bubble sort algorithm would come into play as well. We know that the worst case time complexity of the Bubble sort algorithm is O(n²), which occurs when the elements in the array/list are stored in the reverse order and hence the total number of comparisons needed will be n².
Therefore, we get a total runtime of O(n²).
Average case time complexity
In our bucket sort algorithm, we have four loops (step 1, step 3, step 4 and step 5) which iterate over k buckets and n elements.
The average case occurs when the elements are distributed randomly in the list. Bucket sort runs in linear time in all cases until the sum of the squares of the bucket sizes is linear in the total number of elements.
It takes O(n) time in order for us to assign and store all the elements of the input array into the bucket list.
Since we are using the Bubble sort algorithm to sort each bucket individually, step 4 (from our algorithm) would cost us O(n²) time.
However, we will need to compute its complexity for the average case.
Step 4 (bubble sort sorting) of our algorithm costs:
where nᵢ is the total length of the bucket present at index i and k is the total number of buckets.
Since we are concerned with computing the average time, E(nᵢ²) (expectation) is what we are interested in.
Let Xij be the random variable that is 1 if element j is placed in the bucket i, else it will be 0.
We have the value of nᵢ as:
Hence, we get:
Now the summation has been divided into two cases, which are:
(a) j = k
(b) j ≠ k
Since there are k buckets, the probability that an object is distributed to bucket i is 1/k.
The value of Xij is 1 with probability 1/k else it is 0. Therefore, we get:
Computing it with the summation now, we get:
The complexity then becomes:
As our final step, we have to concatenate our elements back together in the form of an array to produce our final sorted array. Since there are k buckets, this step will cost us a total of O(k) time.
Hence, finally, we come to the conclusion that the average case time complexity for this algorithm will be O(n + n²/k + k).
Keep in mind that if k is chosen to be Θ(n), then bucket sort runs in O(n) average time, provided that we have a uniformly distributed input in the form of an array or list.
Best case time complexity
The best case in Bucket sort occurs when the elements are distributed in a balanced manner across the buckets, i.e., the number of elements spread across in each bucket are identical.
It can get even better depending upon the sorting algorithm that you are using to sort each bucket individually. You can even use different sorting algorithms for different cases. If the elements stored inside the bucket list are already sorted somehow after the partitioning, the complexity will become even better.
Once again, we will have a complexity of O(k) for assigning and pushing elements onto the bucket list and a complexity of O(n) for sorting the elements inside the bucket list.
Hence, we get a total runtime of O(n + k).
Space complexity
The space complexity for Bucket sort is O(n + k), where n is the number of elements and k is the number of buckets.
Hence, the space complexity of this algorithm gets worse with the increase in the size of the input array and the bucket list as well.
Comparison with other sorting algorithms
Let's find out as to how the Bucket sort algorithm fares amongst its other counterpart sorting algorithms.
- It can be said that Bucket sort is a generalization or a slightly modified version of Counting sort. Consider the scenario when each bucket is of size 1, then bucket sort will simply have the same working as that of counting sort.
- In the scenario when the bucket list only consists of two buckets, the algorithm effectively becomes a version of QuickSort where the pivot value is the middle value of the input elements.
- Top-down radix sort can also be categorized as a generalization of bucket sort where both the range of values and the number of buckets in the bucket list are constrained to be a power of two.
With this article at OpenGenus, you must have the complete idea of Time and Space Complexity of Bucket Sort.