A Linked list is a dynamic data structure which can grow or shrink on demand. It is usually implemented using NULLs, we will consider an alternative no NULL approach and use placeholder nodes.

Introduction

A linked list is a dynamic data structure made up of a sequence of nodes. These nodes are not stored contiguously in memory but instead each nodes stores a link to the next node. Thus each node has a link that points to the next node in the list.
In the implementation, the last node usually points to a NULL value. But we will use a placeholder node. The number of nodes in a linked list is not fixed and thus the list can grow or shrink on demand. This dynamic nature is very useful when we need to deal with an unknown number of objects.
A linked list is simply a sequence of nodes. Among all the nodes in the linked list the first node is specified as a head node, and the last node will be the tail node. Note that in-case the list only has one node, the head and tail node will be the same node. To specify these we use head and tail node pointers.

This article covers singly linked list and its implementation in C++.

Node design

A linked list is made up of nodes of the same type. Here we'll assume that we want to store integer values in the linked list. We will consider the nodes to be of two types: list nodes and placeholder nodes.
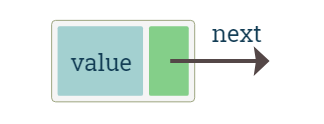
The list nodes each have a data variable called value and a next pointer.
The placeholder nodes are used like the NULL values and are used to indicate the end of the list.

Diagram shows the list node

The list node is implemented as a struct which has an integer value variable alongwith the pointer which will store the address of the next node. For convenience a constructor has also been provided. Note that this is valid in C++.

struct node
{
    int value;
    node* next;
    node(int value): value(value), next(nullptr)
    {
    }
};

A node would be created by dynamic memory allocation. Free memory is allocated using the new operator. We'll use the following helper function to create a node.

node* createNode(int value)
{
    return new node(value);
}

Placeholder node

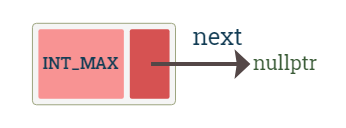
The last element's next pointer points to the placeholder node. This is analogous to the using a NULL value. The palceholder node has the value of INT_MAX. Since we'll be using nodes themselves to indicate the end of the list, we need a way to differentiate them. We could assume that their values are positive infinity (or negative infinity). In this implementation we use use the value of macro INT_MAX defined in the header <climits>.

diagram shows a placeholder node

We use a helper function to create the node. The function returns the address of the newly allocated placeholder node.

static node* getPlaceholderNode()
{
    return new node(INT_MAX);
}

Size of the linked list

The size of the linked list is the number of nodes in the list. To determine the size, we use a size variable. Initially at the time of creation of the linked list the value of this variable is set to 0. The value is incremented when a new node is added to the linked list and decremented when an existing node is deleted from it.
The use of this variable allows us to get the size in O(1) (constant) time by simply returning the value of the variable size. We'll use a function getSize() to return the size.

int getSize()
{
    return this->size;
}

Empty linked list

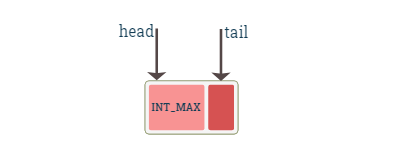
The linked list is empty when there are no nodes in the list. As for our implementation, the empty list will have only a placeholder node and the size of the linked list would be 0. Additionally the head and the tail pointers would point to this placeholder node.

The diagram shows an empty linked list

Inserting a node

We consider three ways to insert a node:

1. At the beginning of the list
2. At the end of the list
3. At any index in the list

Inserting at the beginning of the list

Inserting at the beginning is easy. We allocate a new node and then make its next pointer point to the first node of the existing linked list. Next we make the newly inserted node the new head node of the list.
To insert we can have two cases:

1. The linked list is empty
2. The linked list has one or more nodes

Insertion at the beginning when the list is empty
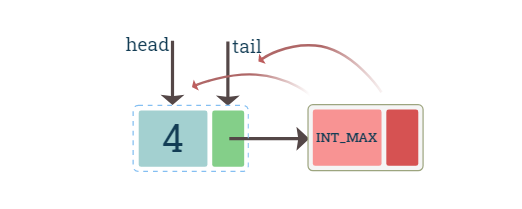
The linked list is empty which means that the list has only a placeholder node. The head and tail pointers point to this node. To insert the node we first create the node, make its next pointer point to the placeholder nodes. Then finally make the head and tail node to point to this newly inserted node. Thus after insertion, this newly created node will be both the head node and the tail node.

Insertion at the beginning when the list is non-empty
The linked list is not empty which means that there is atleast one node. we need to create the node and make its next pointer point the head node. Then make the head pointer point to this newly inserted node. Here we need not change the tail pointer.

Notice that in both the cases, the newly inserted node is made the head node and tail pointer is changed only for the second case. So both cases can be combined and implemented as follows

void add_first(int value)
{
    // create the new node
    node* n = new node(value);
    
    // if list is empty, we have to change tail to point to this new node
    if(isPlaceholderNode(head))
    {
        tail = n;
    }
    
    // in both the cases, the head node will be the newly inserted node
    n->next = head;
    head = n;
    
    // update size
    size++;
}

Inserting at the end of the list

Similar to adding node at front, adding at the end also has two cases:

1. Either the linked list is empty
2. It has one or more nodes

Insertion at the end when the list is empty
This is equivalent to inserting at the beginning when the list is empty.

Insertion at the end when the list is non-empty
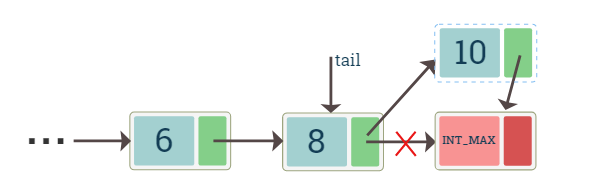
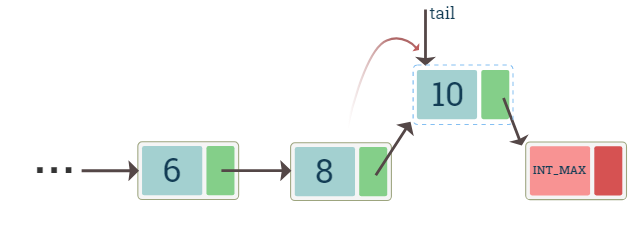
For a non-empty list we need a pointer to both the last node and the placeholder node. For insertion the last node's next pointer would point to the new node and the new node's next pointer will point to the placeholder node.


diagrams show insertion of a node at the end of the list

Both of the above cases can be combined and implemented as follows

void add_last(int value)
{
    // create the new node
    node* n = new node(value);
    
    // if the list is empty
    if(isPlaceholderNode(head) && isPlaceholderNode(tail))
    {
        head = n;
        n->next = tail;
        tail = n;
    }
    else // else list is not empty
    {
        // pn is pointer to the placeholder node
        node* pn = tail->next;
        
        // insert after tail and before placeholder node
        tail->next = n;
        n->next = pn;
        
        // make this node the new tail node
        tail = n;
    }
    // update size
    size++;
}

Deleting a node

Deleting a node is not simple as every node will in addition to value, store the pointer to the next node. If we delete some node directly then the memory address of the next node is lost.

What if the node doesn't exist?
There are multiple ways to handle this. For simplicity, in our implementation we do nothing if a node or a position in the linked list doesn't exist. So if we try to delete a node at position 0 in an empty list, there won't be any error messages. This can be easily changed however.

We consider three cases for the deletion of a node.

1. at the beginning of the linked list
2. at the end of the linked list
3. at any position in the list

Deletion at the beginning

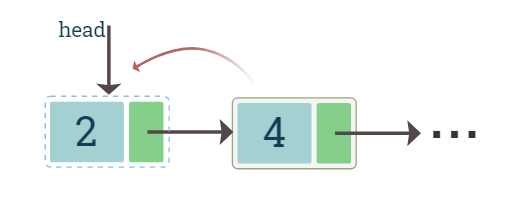
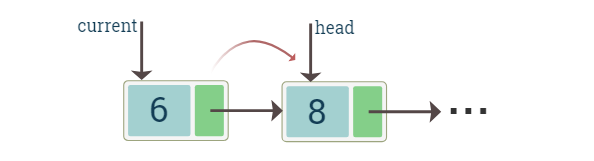
The node that we want to delete is the one that is pointed to by the head pointer. We assign a current pointer to this node and then move the head pointer to the next node. Now the current pointer is pointing to the node that we want to delete and the head pointer is pointing to the new head node. We can now simply delete the current pointer node.

diagram shows deletion of the head node

void remove_first()
{
    if(getSize()>0)
    {
        node* current = head;
        head = head->next;
        delete current;
        if(getSize()==1)
        {
            tail = head;
        }
        size--;
    }
}

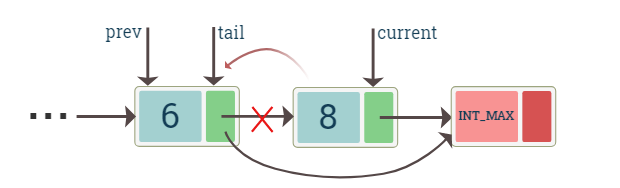
Deletion at the end

To delete the node at the end we first make the current pointer point to it. we also need a pointer to the previous node. To delete we set the next of the previous node to the placeholder node, and then we can simply delete the current node.

The diagram shows the deletion of the tail node

void remove_last()
{
    if(getSize()>0)
    {
        if(getSize()==1)
        {
            node* current = head;
            head = current->next;
            tail = current->next;
            delete current;
            size--;
        }
        else
        {
            node* prev = head;
            for(int i=0; i<getSize()-2; ++i)
            {
                prev = prev->next;
            }
            node* current = prev->next;
            prev->next = current->next;
            tail = prev;
            delete current;
            size--;
        }
    }
}

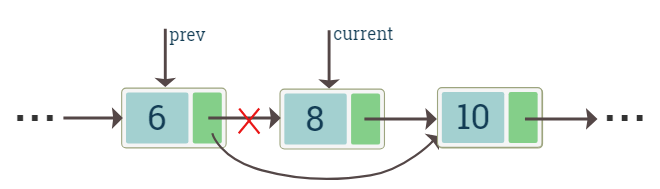
Deletion at any position

If we want to delete a head node (position 0) or the tail node (position size-1) then we can simply use the functions remove_first() and remove_last() respectively.
When we want to delete a node in other positions, we can assume that a previous and next node (to the current node) always exists. We point the prev to the previous node and current to the node that we want to delete. Then next node can be accessed using current->next.
After this we can set the prev's next pointer to the next node, and then simply delete the current node.

The diagram shows deletion of a node

void remove_at(int idx)
{
    if(idx >= 0 && idx < getSize())
    {
        if(idx == 0)
        {
            remove_first();
        }
        else if(idx == getSize()-1)
        {
            remove_last();
        }
        else{
            node* prev = head;
            for(int i = 0; i<idx-1; ++i)
                prev = prev->next;
            node* current = prev->next;
            prev->next = current->next;
            delete current;
            size--;
        }
    }
}

Conclusion

While the important functions were covered for the placeholder nodes based Linked list. We can add a constructor and destructor and other functions. The complete implementation is at https://github.com/RohitTopi/opengenus/blob/main/Linked_list_no_NULL.cpp