Check if a Binary Tree is Balanced by Height

Binary tree is a special type of data structure that has collection of elements known as nodes. The topmost node is called parent node. Each node has either zero, one or two child nodes. A node with zero children is called Leaf Node or Terminal Node.

In this article, we will explore the algorithm to check if a Binary Tree is balanced by height or not.

Terminologies:

Based on below image let us understand some important terminologies:

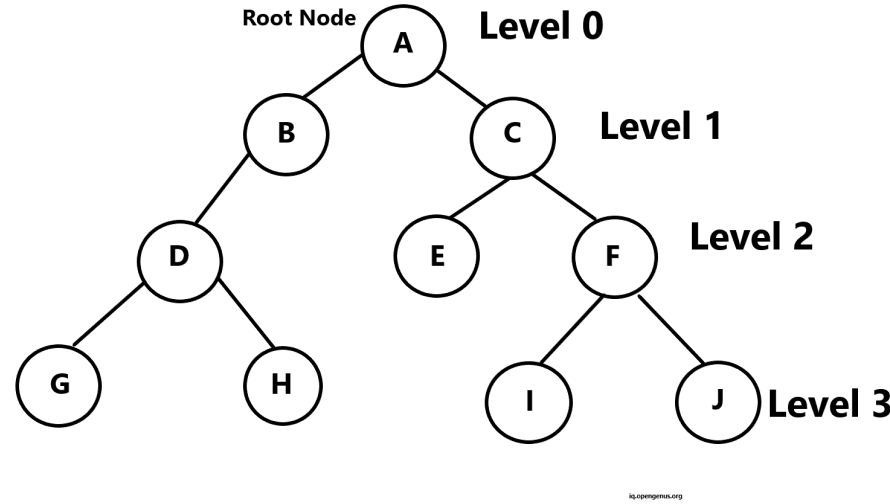
1. Parent :

If any node has a child node on left and/or right then that node is called the parent node to those successor child nodes. All nodes except root node have a parent node.

Example: A is the parent node to node B and C.

2. Level Number:

Each node have a level number in binary tree starting from the root node at level 0. Every child node has parent's level number + 1.

Example: B and C are at Level 1 whereas their parent node A is at Level 0.

3. Degree of a node:

The degree of a node is the number of children of that node. Hence, the degree of leaf node is 0.

Example: Node E in above image has degree 0. However, node A has degree 2.

4. Siblings of Node:

All nodes at the same level with same parent are siblings.

Example: Node G and H are siblings since they are both at Level 3 and have common parent D.

5. Leaf Node:

Any node with no children is leaf or terminal node.
Example: Node E, G, H, I and J are leaf nodes.

6. Edge:

An edge is a line connecting a node to its successor nodes. A binary tree of n nodes has exactly n-1 edges. The reason behind it is that except root node, all other nodes are connected to their parent node via edges.

7. Path:

The sequence of consecutive edges is known as a Path of the node.
Example: The path from node G is node D, node B and node A.

8. Depth:

The length of the path from the root node to the given node is called depth of that node.
Example: Depth of node A is 0 since it is the root node itself.

9. Height of the tree:

It is the length from the root node till the node of maximum depth. If the height of any tree is "h" then it can have h nodes or at most 2h-1 nodes.
The height of a binary tree with n nodes is at least log2(n+1) and at most n.
Example: Height of above tree is 3.

Below is the figure of the binary tree.

Here, Node 1 is the root node. The left-subtree consists of node 2, 4 and 7. The right subtree consists of node 3, 5, 6 and 8. Node 1 has two successors node 2 and 3. Whereas, node 7, 5 and 8 have no successor nodes. Hence, they have empty sub-trees.

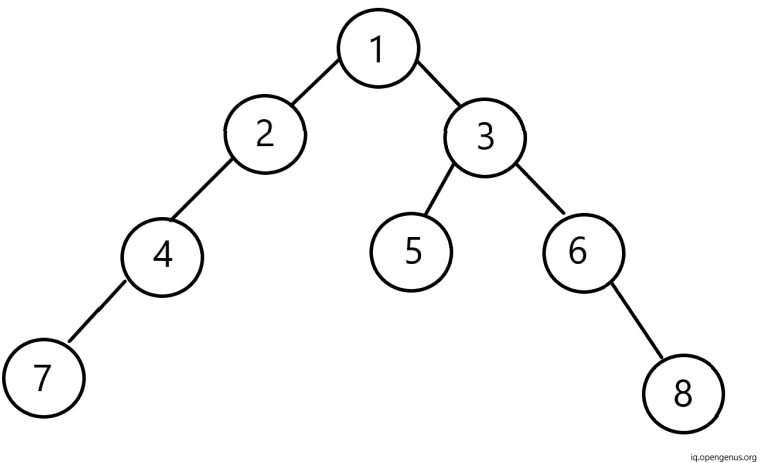
The root pointer points to the root node. Further, every element has a data element with left pointer, pointing to the left node and right pointer, pointing to the right node respectively.

Checking if a binary tree is balanced:

A tree is said to be balance if:

1. The left subtree is balanced for each node.
2. Right subtree is also balanced for each node.
3. The absolute height difference of left and right subtree is not more than 1.

Further,all empty trees are always height balanced.

Algorithm:

Step 1: Start
Step 2: If the node is NULL then return 0.
Step 3: If left sub tree is not balanced then return -1.
Step 4: If the right sub tree is not balanced then return -1.
Step 5: If the absolute difference between height of left and right subtree is greater than 1,return -1 else return maximum out of left and right subtree's height + 1.
Step 6: End.

Example:
Considering the binary tree below,

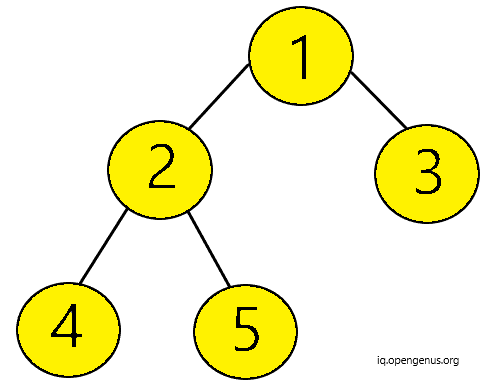
Firstly, our node is not NULL.
Hence, we proceed to check the height of left subtree first.

1. For the root node, the height of its left subtree is 2 (from node 1 to node 2 and node 2 to node 4). Similarly, the height of the right subtree is 1 (from node 1 to node 3). So, absolute difference in the height of left and right subtree is 1.
Hence, satisfying the condition that absolute difference of the height of left and right subtree is smaller than or equal to 1.

2. Similarly,for the node 2 the height of its left subtree is 1 (node 2 to node 4) and height of right subtree is also 1 (node 2 to node 5). Hence, the absolute difference of their heights is 0.
Hence, satisfying the condition that absolute difference of the height of left and right subtree is smaller than or equal to 1.

3. For node 4, node 5 and node 3 the absolute difference in their left and right subtrees is 0 since they do not have any children nodes.
Hence, satisfying the condition that absolute difference of the height of left and right subtree is smaller than or equal to 1.

This way all nodes satisfy the required condition. Hence, our binary tree is balanced.

Let us implement it via code :

//Assuming the node of the binary tree is already defined
// Function to check if a binary tree is balanced by height
class sol{
public:
// firstly, pass the root as argument to "balanced" function
int balanced(Node* root)
{

// if the root is NULL return 0

if(root==NULL)return 0;

//check if the left subtree's height is balanced. If no then return -1

int leftheight = balanced(root ->left);
if(leftheight == -1)return -1;

//check if the right subtree's height is balanced. If no then return -1

int rightheight = balanced(root->right);
if(rightheight == -1)return -1;

//if absolute difference of left subtree's height and right subtree's height > 1 then return -1

if(abs(rightheight-leftheight)>1) return -1;

// return maximum out of left subtree's height and right subtree's height + 1

return max(leftheight,rightheight)+1;
}

bool bal(Node *root) {
        return balanced(root) != -1;
    }
};

The time complexity of this approach is O(n).

Hence using the above described approach in Opengenus article you can easily find out if a binary tree is balanced by height or not.