
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will learn how to find the mirror image of a point (x,y,z) in 3D-plane.
Table of contents:
- Equation of plane in 3-Dimension
- Implementation
- Steps
- Code
- Output
- Time Complexity
Prerequisite: Find mirror image of point in 2D plane
Equation of plane in 3-Dimension
a. x + b. y + c. z + d = 0
where,
a,b,c = directions ratios of normal to the plane
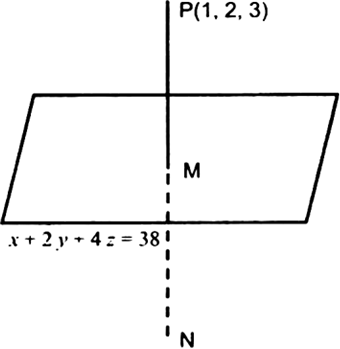
Point P(x1,y1,z1) :
Assume a point P(x1,y1,z1) in the 3D plane.
Direction ratios relation :
(x - x1) / a = (y - y1) / b = (z - z1) / c = k
Line equation in terms of k and x1,y1,z1 :
a * (a * k + x1) + b * (b * k + y1) + c * (c * k + z1) + d = 0
From the above equation we can find value of k in terms of directions ratios and x1,y1,z1 :
k = (-a * x1 - b * y1 - c * z1 - d) / (a * a + b * b + c * c)
Cordinates of point on the plane M(x2,y2,z2) which is exactly at the middle of the line joining mirror image and real point and is present on the mirror plane is given as :
x2 = a * k + x1
y2 = b * k + y1
z2 = c * k + z1
Mirror image equation N(x3,y3,z3) :
x3 = 2 * x2 - x1
y3 = 2 * y2 - y1
z3 = 2 * z2 - z1
Implementation
1.Create a function which finds the k value using the equation above and point P(x1,y1,z1).
2.Find M(x2,y2,z2) values of point on the mirror plane using k.
3.Finally find N(x3,y3,z3) values of mirror image using k and M(x2,y2,z2).
4.Direction ratios for the plane can be assigned in the driver code.
5.Take input (x1,y1,z1) and output the mirror image (x3,y3,z3).
Steps
1.Function call with values :
a = 1 ; b = -2 ; c = 0 ; d = 0
x1 = 1 ; y1 = 5 ; z1 = 1
mirror_image(a,b,c,d,x1,y1,z1) = mirror_image(1,-2,0,0,1,5,1)
2.Inside the function
- Calculating k using the formula
k = (-a * x1-b * y1-c * z1-d)/float((a * a + b * b + c * c))
k = 1.8
- Calculating (x2,y2,z2)
x2 = a * k + x1
x2 = 1 * 1.8 + 1
y2 = b * k + y1
y2 = -2 * 1.8 + 5
z2 = c * k + z1
z2 = 0 * 1.8 + 1
value (x2,y2,z2) :
x2 = 2.8
y2 = 1.4
z2 = 1.0 - Calculating mirror image (x3,y3,z3)
x3 = 2 * x2-x1
x3 = 2 * 2.8 - 1.0
y3 = 2 * y2-y1
y3 = 2 * 1.4 - 5
z3 = 2 * z2-z1
z3 = 2 * 1.0 - 1.0
mirror image :
x3 = 4.6
y3 = -2.2
z3 = 1.0
Code
def mirror_image(a, b, c, d, x1, y1, z1):
k =(-a * x1-b * y1-c * z1-d)/float((a * a + b * b + c * c))
x2 = a * k + x1
y2 = b * k + y1
z2 = c * k + z1
x3 = 2 * x2-x1
y3 = 2 * y2-y1
z3 = 2 * z2-z1
print("mirror image of point P(",x1,",",y1,",",z1,") is :")
print("x3 =",x3)
print("y3 =",y3)
print("z3 =",z3)
a = 1 ; b = -2 ; c = 0 ; d = 0
x1 = 1 ; y1 = 5 ; z1 = 1
mirror_image(a, b, c, d, x1, y1, z1)
Output
mirror image of point P( 1 , 5 , 1 ) is :
x3 = 4.6
y3 = -2.2
z3 = 1.0
Time Complexity
Addition Time Complexity :
In usual practice we assume addition time complexity to be O(1) but acutally the complexity of additon depends on the greater number.(Being more precise it depends on number of bits in its binary representation)
Note : A number N has log(N) bits in its binary representation.
Time complexity : O(log(N))
Assumed Time Complexity : O(1)
How O(1) then?
In real systems bitwise operations are processed parallely and each operation take O(1) time so total time taken will be the same as O(1)
Multiplication Time Complexity :
In usual practice we assume multiplication time complexity to be O(1) but acutally the complexity of multiplication is more complex than addition and subtraction, and it takes O(NlogN) time where N is the number of digits in the number.
Total Time Complexity of the algorithm :
O(NlogN) + O(logN)
We can assume it as O(NlogN) as it is of higher order but, in real systems we will ignore the time taken for arithmetic operations because the numbers are finite and given beforehand and is not a variable so we consider it in O(1) constant time.
