Threaded Binary Tree

What is threaded binary tree?

Threaded binary tree is a simple binary tree but they have a speciality that null pointers of leaf node of the binary tree is set to inorder predecessor or inorder successor.

The main idea behind setting such a structure is to make the inorder and preorder traversal of the tree faster without using any additional data structure(e.g auxilary stack) or memory to do the traversal.

Types of Threaded Binary Tree

There are two types of threaded binary tree:

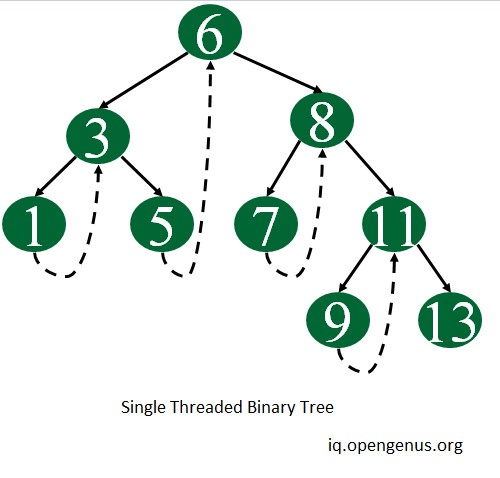
1. Single Threaded Binary Tree

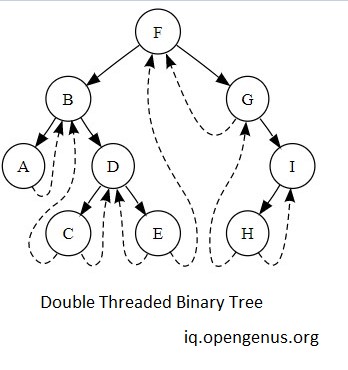
2. Double Threaded Binary Tree

3. Single Threaded Binary Tree: Here only the right NULL pointer are made to point to inorder successor.

4. Double Threaded Binary Tree: Here both the right as well as the left NULL pointers are made to point inorder successor and inorder predecessor respectively. (here the left threads are helpful in reverse inorder traveral of the tree )

Structure of node in threaded binary tree

A node in threaded binary tree has two additional attributes:

• rightThread
• leftThread

Both new attributes are of type bolean.

Following is the node structure in a Single threaded binary tree and Double threaded binary tree:

// single threaded

struct Node{
   int data ;
   Node *left ;
   Node *right ;
   bool rightThread ;
}

// double threaded

struct Node{
   int data ;
   Node *left ;
   Node *right ;
   bool leftThread ;
   bool rightThread ;
}

Significance of bool variable (leftThread and rightThread) in structure

if we have some address stored in some node to diffrentiate whether that address is of parent node or of child node we use leftThread and rightThread bool variables.

leftThread and rightThread bool variables stores whether left and right pointers point to child node or some ancestor node , if the bool variable is set to true that means pointer is pointing to child node and if it is set to 1 that means that pointer is pointing to parent node.

for example:

let's us say for some node right pointer is pointing to some node and righThread is set to true, this means that it is pointing to it's children, but if in the same case if rightThread is set to false this means that it is pointing to it's parent node (and not child ).

What happens with righmost and leftmost null nodes ?

when we create a threaded binary tree the left most and rightmost pointers do not have inorder predecessor or inorder successor so they are made to point to a dummy node as you can see in the image and leftThread of leftmost node and rightThread of rightmost node is set to false.

Operations in Threaded Binary Tree

We can also perform various operations in a threaded binary tree like -

1.Insert
2.search
3.Delete

After performing the following operations we need to make sure that our new binary tree still follows all the conditions of a threaded binary tree and also these operations should be performed with least amount of space and time complexity possible.

so, for understanding all the three operations you can view article given below -

Operations in Threaded Binary Tree

Applications of Threaded Binary Tree

The idea of threaded binary trees is to make inorder traversal of the binary tree faster and do it without using any extra space, so sometimes in small systems where hardware is very limited we use threaded binary tree for better efficiency of the software in a limited hardware space.

Time and space complexity for operations

Time complexity for

• for insertion : log(n)
• for deletion : log(n)
• for seaching : log(n)

space complexity for insertion is O(1) , for deletion and searching we donot require any extra space.

the time required for finding inorder predecessor or successor for a given node is O(1) provided we are on that node.

To understand these operations better with code explanation you can follow the link given in operations in threaded binary tree section.

Code for threaded binary tree and all operations

#include <bits/stdc++.h>
using namespace std;

struct Node {
   struct Node *left, *right;
   int info;

   // True if left pointer points to predecessor
   // in Inorder Traversal
   bool lthread;

   // True if right pointer points to predecessor
   // in Inorder Traversal
   bool rthread;
};

struct Node *search( struct Node *root , int key ){

    Node *ptr = root ;

    

    while( ptr != nullptr  ){

        if( ptr->info == key ){
            // indicating that the element is found then
            return ptr ;
        }else if( ptr->info < key ){
            // moving to inorder predecessor of the current node 
            ptr = ptr->right ;
        }else{
            // moving to inorder successor of the current node
           ptr = ptr->left ;
        }

    }

    // if element is not found then we can return nullptr indicating element not 
    // found in the given binary search tree
    return nullptr ;

} 

// Insert a Node in Binary Threaded Tree
struct Node* insert(struct Node* root, int ikey)
{
   // Searching for a Node with given value
   Node* ptr = root;
   Node* par = NULL; // Parent of key to be inserted
   while (ptr != NULL) {
       // If key already exists, return
       if (ikey == (ptr->info)) {
           printf("Duplicate Key !\n");
           return root;
       }

       par = ptr; // Update parent pointer

       // Moving on left subtree.
       if (ikey < ptr->info) {
           if (ptr->lthread == false)
               ptr = ptr->left;
           else
               break;
       }

       // Moving on right subtree.
       else {
           if (ptr->rthread == false)
               ptr = ptr->right;
           else
               break;
       }
   }

   // Create a new Node
   Node* tmp = new Node;
   tmp->info = ikey;
   tmp->lthread = true;
   tmp->rthread = true;

   if (par == NULL) {
       root = tmp;
       tmp->left = NULL;
       tmp->right = NULL;
   }
   else if (ikey < (par->info)) {
       tmp->left = par->left;
       tmp->right = par;
       par->lthread = false;
       par->left = tmp;
   }
   else {
       tmp->left = par;
       tmp->right = par->right;
       par->rthread = false;
       par->right = tmp;
   }

   return root;
}

// Returns inorder successor using left
// and right children (Used in deletion)
struct Node* inSucc(struct Node* ptr)
{
   if (ptr->rthread == true)
       return ptr->right;

   ptr = ptr->right;
   while (ptr->lthread == false)
       ptr = ptr->left;

   return ptr;
}

// Returns inorder successor using rthread
// (Used in inorder)
struct Node* inorderSuccessor(struct Node* ptr)
{
   // If rthread is set, we can quickly find
   if (ptr->rthread == true)
       return ptr->right;

   // Else return leftmost child of right subtree
   ptr = ptr->right;
   while (ptr->lthread == false)
       ptr = ptr->left;
   return ptr;
}

// Printing the threaded tree
void inorder(struct Node* root)
{
   if (root == NULL)
       printf("Tree is empty");

   // Reach leftmost Node
   struct Node* ptr = root;
   while (ptr->lthread == false)
       ptr = ptr->left;

   // One by one print successors
   while (ptr != NULL) {
       printf("%d ", ptr->info);
       ptr = inorderSuccessor(ptr);
   }
}

struct Node* inPred(struct Node* ptr)
{
   if (ptr->lthread == true)
       return ptr->left;

   ptr = ptr->left;
   while (ptr->rthread == false)
       ptr = ptr->right;
   return ptr;
}

// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case1(struct Node* root, struct Node* par,
                  struct Node* ptr)
{
   // If Node to be deleted is root
   if (par == NULL)
       root = NULL;

   // If Node to be deleted is left
   // of its parent
   else if (ptr == par->left) {
       par->lthread = true;
       par->left = ptr->left;
   }
   else {
       par->rthread = true;
       par->right = ptr->right;
   }

   // Free memory and return new root
   free(ptr);
   return root;
}

// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case2(struct Node* root, struct Node* par,
                  struct Node* ptr)
{
   struct Node* child;

   // Initialize child Node to be deleted has
   // left child.
   if (ptr->lthread == false)
       child = ptr->left;

   // Node to be deleted has right child.
   else
       child = ptr->right;

   // Node to be deleted is root Node.
   if (par == NULL)
       root = child;

   // Node is left child of its parent.
   else if (ptr == par->left)
       par->left = child;
   else
       par->right = child;

   // Find successor and predecessor
   Node* s = inSucc(ptr);
   Node* p = inPred(ptr);

   // If ptr has left subtree.
   if (ptr->lthread == false)
       p->right = s;

   // If ptr has right subtree.
   else {
       if (ptr->rthread == false)
           s->left = p;
   }

   free(ptr);
   return root;
}

// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case3(struct Node* root, struct Node* par,
                  struct Node* ptr)
{
   // Find inorder successor and its parent.
   struct Node* parsucc = ptr;
   struct Node* succ = ptr->right;

   // Find leftmost child of successor
   while (succ->lthread==false) {
       parsucc = succ;
       succ = succ->left;
   }

   ptr->info = succ->info;

   if (succ->lthread == true && succ->rthread == true)
       root = case1(root, parsucc, succ);
   else
       root = case2(root, parsucc, succ);

   return root;
}

// Deletes a key from threaded BST with given root and
// returns new root of BST.
struct Node* deleteFromThreadedBst(struct Node* root, int target)
{
   // Initialize parent as NULL and
   // Node as root.
   struct Node *par = NULL, *ptr = root;

   // Set true if key is found
   int found = 0;

   // Search key in BST : find Node and its
   // parent.
   while (ptr != NULL) {
       if (target == ptr->info) {
           found = 1;
           break;
       }
       par = ptr;
       if (target < ptr->info) {
           if (ptr->lthread == false)
               ptr = ptr->left;
           else
               break;
       }
       else {
           if (ptr->rthread == false)
               ptr = ptr->right;
           else
               break;
       }
   }

   if (found == 0)
       printf("target not present in tree\n");

   // Two Children
   else if (ptr->lthread == false && ptr->rthread == false)
       root = case3(root, par, ptr);

   // Only Left Child
   else if (ptr->lthread == false)
       root = case2(root, par, ptr);

   // Only Right Child
   else if (ptr->rthread == false)
       root = case2(root, par, ptr);

   // No child
   else
       root = case1(root, par, ptr);

   return root;
}

// Driver Program
int main()
{
   struct Node* root = NULL , *temp = NULL;

   root = insert(root, 1);
   root = insert(root, 3);
   root = insert(root, 5);
   root = insert(root, 7);
   root = insert(root, 12);
   root = insert(root, 2);
   root = insert(root, 10);
   root = insert(root, 6);
   
   temp = search(root , 5) ;

   if( temp ) cout<<"Element with value 5 found\n" ;
   else cout<<"element doesn't exist in the given binary threaded tree\n" ;

   root = deleteFromThreadedBst(root, 6);
   inorder(root);

   return 0;
}

Following is the output of the above code:

Element with value 5 found
1 2 3 5 7 10 12

Thank you for reading!!