
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be discussing how to find the diameter of a tree or in general a graph. The algorithm that we will be using to find the diameter of the tree is Depth first search.
if you are unfamiliar with depth first search (DFS), I would first suggest you to go through this article before proceeding: https://iq.opengenus.org/depth-first-search/
What is Diameter of a tree ?
Diameter of tree is defined as the no. of nodes in the longest path between leaf nodes nodes of a tree ( undirected graph ) , it is also called the width of the tree.
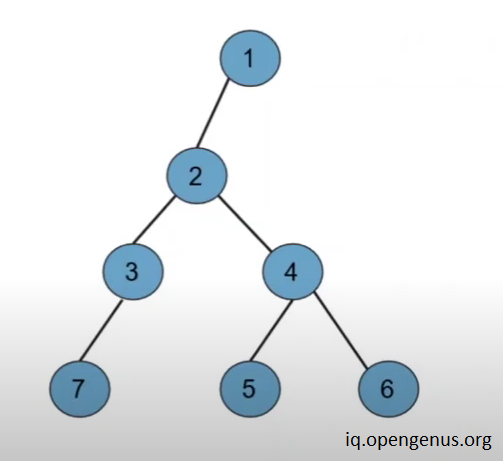
for example -
In the tree shown above the diameter of the tree is no. of nodes coming along the path 7-3-2-4-6 or 7-3-2-4-5.
How to find diameter of the tree ?
Novice Approach
1.We can run DFS n times .
2.first we can choose any node and find the farthest node from that node using depth first search .
3.we need to repeat the step 2 with all the nodes of the tree and store the maximum value .
4.This maximum value will then be the diameter of the tree.
Time Complexity
The above approach would work fine but time complexity for the above approach will be O(n*n) which is quite high.
Better Approach
we can find the diameter of any tree using only 2 DFS run.
how ?
Quick Explanation -
1.Take any arbitary node as the root node .
2.Run dfs from that node and find the farthest node.
3.let this node be x .
4.Now run dfs from this node to the farthest away node , let this node be y.
5.now the count of all the nodes that come along the way of x and y ( including them) is the diameter of the tree.
Why this works ?
whenever we run DFS we always reach one of the end points of diameter of the tree and from that node we are just finding the farthest node which turns out to be the diameter of the tree.
Let us proof this fact that on running DFS we always reach the end point of diameter of the tree
Proof
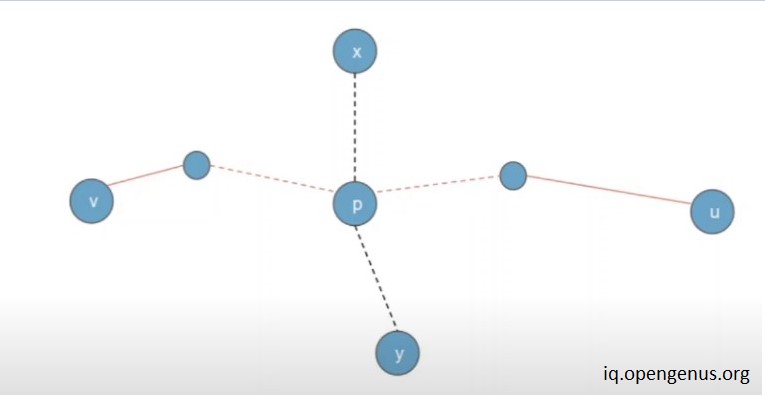
Proof by contradiction
here we are considering x as the root of the tree
Assume that on running DFS first time from x and finding the farthest node we reach on node y .
Let's say y is not the end point of the diameter of the tree
and v-p-y is the actual diameter of the tree
In that case according to the above image we can write the equation
( note that if root of the tree lies on the diameter of the tree then distance xp is considered as 0 )
xp + py < xp + pv
and
xp + py < xp + pu
on simplying the above equations
py < pv
and
py < pu
but this cannot be true as y is at maximum distance from p and according to our assumption y is not on the diameter of the tree both statements cannot be true simultaneously .
so, our first assumption that node y doesnot lie on the diameter doesnot hold true and hence after running the first DFS we reach node y which always lie on the diameter of the tree .
Example
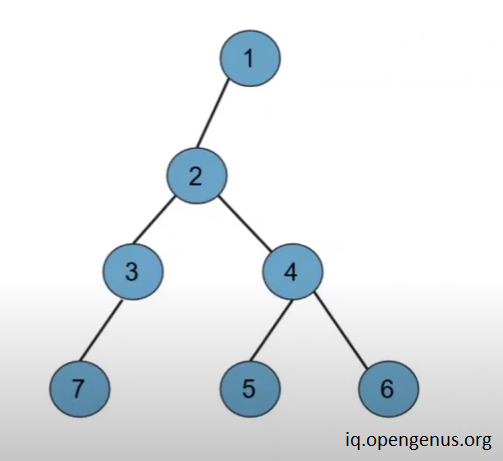
Suppose we want to find the diameter of the graph shown in the above image.
- let us take node 4 as our starting node ( we can choose any node )
- Now on running the depth first search for the first time we will be able to find the one end of the diameter which will be 7 for this example .
- Now on running DFS from 7 and finding the farthest node we will reach 6 via path
7-3-2-4-6.
4.The count of nodes along the path is 5 which is the diameter of the tree in this example.
( Note - we could have also reached 6 via path 7-3-2-4-5 which would also have been the diameter of the tree as both count as farthest node with same value of distances )
5.In this way we can find the diameter of any tree using only two DFS run .
Code
#include <iostream>
#include<vector>
using namespace std;
// here maxD represent the diameter of the tree
int maxD = -1 , maxNode = -1 ;
// maxNode represents node at maximum distance
// declaring the visited node as we will be using the DFS
int vis[8] ;
void createEdge( int a , int b , vector<int> graph[] ){
// creating undireted edges between the connected nodes
graph[a].push_back(b) ;
graph[b].push_back(a) ;
}
void DFS( vector<int> graph[] , int node , int d )
{
// marking the node as visited
vis[node] = 1 ;
// if the distance from root is greater then maximum Distance then updating the maximum value of distance
// also storing the maxNode no. as this node is now at the farthest distance
if( d > maxD )
{
maxNode = node ;
maxD = d ;
}
// applying the standard dfs
for( auto x : graph[node] )
{
if( vis[x] == 0 )
{
DFS( graph , x , d+1 ) ;
}
}
}
int main()
{
// first creating the nodes of the graph
vector<int> graph[8] ;
// now creating the edges of the tree as shown in the image of this article
createEdge( 1 , 2 , graph ) ;
createEdge( 2 , 3 , graph ) ;
createEdge( 3 , 7 , graph ) ;
createEdge( 2 , 4 , graph ) ;
createEdge( 4 , 5 , graph ) ;
createEdge( 4 , 6 , graph ) ;
// Applyting DFS from node 1
DFS( graph , 1 , 1 ) ;
// we could have choosen any node in the graph but for simplicity we have choosen node 1
// making every node unvisited as we will be applying DFS
maxD = -1 ;
for( int i = 1 ; i<=8 ; i++ )
{
vis[i] = 0 ;
}
// applying the dfs for the second time as this will give the diameter of the tree
DFS( graph , maxNode , 1 ) ;
// Now printing the maximum diameter of the tree
cout<<maxD<<" is the diameter of the tree "<<endl;
return 0;
}
Output
5 is the diameter of the tree
Complexity Analysis
Time taken = 2 * n ( here n units of time is taken to run the depth first search once)
so -
Time Complexity: O(n).
There is no extra space required apart from some variables therefore the space required is constant.
Space Complexity: O(1).
