In this article, we have considered around 80 questions covering conceptual as well as practical foundations of NumPy to help you in dealing with arrays of homogeneous type.

Multiple Choice Questions:-

1. On what types of elements do numpy work upon ?

a) Heterogeneous.

b) Homogeneous.

c) They can be heterogeneous given the elements follow a certain record type structure like in the excel sheet.(Structured array).

d) Both (b) and (c) are true.

Ans:- d).

Explanation:- Numpy arrays can either be homogeneous or can be heterogeneous given they are written in the format of structured arrays.

2. What would be the result of this line of code:-

np.array([3.14,4,2,7])

a) It will give an error, as every element is not of the same data type.

b) Other values will be upcasted and the result would be array([3.14,4. ,2. ,7.])

c) Floating point value will get truncated with result array([3,4,2,7])

d) Can't be said anything as it may give undefined behaviour.

Ans:- b)

Explanation:- NumPy will upcast if possible like in this case, rest of the integer values are upcasted to floating point values, but had it been a string in place of floating point it would have shown an error.

3. What does dtype argument of numpy.array() specify and what type of value does it take?

a) It can be used to specify the data type of all the elements of the array, and it takes only a string as a parameter.

b) It is used to give the size of the array.

c) It can be used to specify the data type of all the elements of the array, and it takes only associated numpy object.

d) It can be used to specify the data type of all the elements of the array, and it takes both a string as well as associated numpy object as its parameter.

Ans:- d)

Explanation:- np.zeros(10, dtype='int16') Or using the associated NumPy object: np.zeros(10, dtype=np.int16), both will create the same numPy array.

4. How is data in complex128 data type stored?

a) It is represented by a 128 bit float

b) It is represented by two 64 bit floats.

c) It is represented by two 128 bit floats.

d) It is represented by a 64 bit float.

Ans:- b)

Explanation:- Two 64 bits float are used to represent a complex number one 64 for real part and another 64 for imaginary part of the number.

5. What is the output of np.linspace(0,20,5)?

a) array([ 0, 4, 8, 12 , 16])

b) array([ 0, 5, 10, 15])

Ans:- a)

Explanation:- np.linspace(start,stop,number_of_elements) takes attributes in this order.

6. How to create identity matrix using NumPy of n* n dimension?

a) np.eye(n).

b) np.I(n)

c)np.identity(n)

Ans:- a)

Explanation:- np.eye(3) creates
array([[ 1., 0., 0.],
[ 0., 1., 0.], [ 0., 0., 1.]]),following similar pattern np.eye(n) would create n * n identity matrix.

7. How to create uninitialized array of n integers?

a) np.empty(n).

b) np.empty(n, dtype='int64')

c) np.empty(n, dtype=np.int64)

d) Both b) and c).

Ans:- d)

Explanation:- Both methods can be used.

8. How to create an array containing values which are normally distributed with dimension (n,n)?

a) np.random.normal(mean_value, standard_deviation,(n,n))

b) np.random.random(mean_value, standard_deviation,(n,n))

c) np.random.randint(mean_value, standard_deviation,(n,n))

d) None of the above

Ans:- a)

Explanation:- np.random.normal() is the function to create array with normally distributed values.

9. Which method is used to change the data type of an array from one dtype to another?

a) Using ndarray's astype method

b) Using ndarray's dtype method

Ans:- a)

Explanation:- arr = np.array([3.7, -1.2, -2.6, 0.5, 12.9, 10.1]) new_arr=arr.astype(np.int32) will convert the floating point to integer type array, and it can only be used where casting is possible like it can't convert string to floats, and thus, would raise an error.

10. Which method will save the state of randomness and will generate the same random values at each execution?

a) np.random.seed(1).

b) np.random.seed().

c) np,random.seed(2).

d) Both a) and c).

Ans:- d)

Explanation:- np.random.seed(n)
where 'n' is any integer value will be used ot generate the same random values at each execution.

11. Which method can be used to acces an element of a 2-dimensional NumPy array?

a) array[x1][x2]

b) array[x1,x2]

c) array[x1:x2]

d) Both a) and b).

Ans:- d)

Explanation:- Both methods can be used to access an elements of NumPy array given x1 and x2 stay in limits of respective indices.

12. What will be the result of the following code snippet:-

x=np.array([1,2,3,4,5])
x[::-1]

a) array([5,4,3,2,1])

b) array([1,5,4,3,2])

c) array([5,1,2,3,4])

Ans:- a)

Explanation:- Negative indices reverse the position of default start and stop value.

13. How can slicing be applied on 2-d NumPy arrays?

a) array[start_axis1:stop_axis1:step_axis1, start_axis2:stop_axis2:step_axis2]

b) array[start_axis1:stop_axis1:step_axis1] [start_axis2:stop_axis2:step_axis2]

c) Both

Ans:- c)

Explanation:- Both are the ways by which we can slice the 2-d array according to the values of start, stop and step.

14. What will be the output of np.array(array([1,2,3,4,0]),dtype='bool_')

a) array([True,True, True, True, False])

b) array([True,False,False,False,False])

c) array([False,False,False,False,True])

d) array([False,True,True,True,True])

Ans:- a)

Explanation:- For NumPy arrays everything else except '0' is a true.

15. Which method can be used to create an array of zeros?

a) np.zero()

b) np.empty()

c) np.eye()

d) np.zeros()

Ans:- d)

Explanation:- np.zeros(shape_of_array) will create an array of zeros at every position of required sizes.

16. What does the itemsize attribute of a NumPy array mean?

a) It is the size in bytes of an element in the array.

b) It is the size of the array.

c) It is the size in bytes which the array occupies

d) None of the above.

Ans:- a)

Explanation:- itemsize attribute of a NumPy array simply indicates the size of an element of the array which it occupies in the memory, like itemsize for an array containing int64 element would be 8 bytes.

17. What does it mean when we say that slicing creates a view of that array?

a) Changes made to sliced part will get reflected to the original array.

b) Changes made to sliced part will have no impact on the original array and it is just for viewing and no operation can be done over it.

c) It simply means a copy of that array.

d) NOne of the above.

Ans:- a)

Explanation:- Views are a uniques way to analyze and manipulate only a section of the array, and make changes to it.

18. What does np.vstack method do?

a) It is used to concatenate two arrays vertically.

b) It is used to concatenate two arrays horizontally.

c) It is used to concatenate two arrays along axis 1.

d) It is used to concatenate two arrays along axis 0.

Ans:- d)

Explanation:- While concatenating along axis 0, it can easily be accomplished by using np.vstack, i.e. outermost index in a 2-d array.

19. Is '+' operator in Python a wrapper around specific functions built into NumPy?

a) Yes.

b) No.

c) Python's implementation is entirely different from NumPy's implementation.

Ans:- a)

Explanation:- All the Python arithmetic operators are convenient wrappers built into NumPy.

20. What is the Python wrapper for np.mod NumPy ufunc?

a) %

b) //

c) /

d) *

Ans:- a)

Explanation:- '%' operator is the convenient wrapper built into NumPy.

21. What is the NumPy ufunc for calculating sine inverse ?

a) np.arcsin(array_name)

b) np.sineinverse(array_name)

c) np.sininv(array_name)

d) None of the aboove.

Ans:- a)

Explanation:- np.arcsin(array_name) calculates the sine inverse for every value in the array.

22. How to calculate the inverse of logarithm?

a) np.exp(array_name)

b) np.loginverse(array_name)

c) np.loginv(array_name)

d) None of the aboove.

Ans:- a)

Explanation:- np.exp(array_name) can be used to calculate the inverse of logarithm as, exponent and logarithms are inverse functions of each other.

23. What is the NaN-safe counterpart of function np.argmax?

a) There is no NaN-safe function for it.

b) np.nanargmax.

c) np.naargmax.

d) None of the aboove.

Ans:- b)

Explanation:- np.nanargmax(array_name) is the function which takes care of the missing values if any in the array.

24. What will be the dimension of the output array if two arrays having shapes (4,1,2) and (1,3,1) are being operated together by some operand?

a) (4,3,2)

b) There will be an error.

c) (4,3,1).

d) (4,1,2).

Ans:- a)

Explanation:- Its shape will be (4,3,2) when two arrays are broadcasted.(See the rules of broadcasting explained later in this sheet).

25. Which function can be used to check whether any of the values is true or not using NumPy?

a) ap.all()

b) np.each()

c) np.any()

d) np.every()

Ans:- c)

Explanation:- np.any(some_condition) is used to check whether any element follow the given condition inside the parenthesis or not.

Short Answer Questions(Mainly single line coding questions):-

1. Create a NumPy array of 10 even numbers ?

Ans:-

import numpy as np
np.arange(0,20,2)

import numpy as np, makes NumPy available for use, while np.arange(start,stop,step) is used to generate numbers which are greater than equal to start but less than stop with each number's increment equal to step value.

2. Using nested list comprehension create a multidimensional array?

Ans:-

import numpy as np
np.array([[1,2,3] for i in range(0,3)])

Just like in Python lists we can use list comprehension to create new multidimensional array.

3. Calculate the itemsize and array size in bytes of a NumPy array?

Ans:-

import numpy as np
arr=np.array([[1,2,3] for i in range(0,3)])
print("itemsize:", a.itemsize, "bytes")# It will show itemsize
print("nbytes:", a.nbytes, "bytes")# It will show array size

itemsize shows the size occupied by an element wile to calculate the total size occupied ny the array we need to use the nbytes attribute.

4. Show how you will access every element of a 2-d array except the outer rectangle of it?

Ans:-

import numpy as np
arr=np.array([[1,2,3,4] for i in range(0,4)])
arr[1:3,1:3]

A general rule would be arr[1:size_in_axis_1 -1,1:size_in_axis_0 -1].
Similarly, for n-dimensional array, more indices for each axis but with the same pattern would be added.
For 3-d it would be arr[1:size_in_axis_2-1,1:size_in_axis_1 -1,1:size_in_axis_0 -1].

5. How to copy an array ?

Ans:-

import numpy as np
arr=np.array([[1,2,3,4] for i in range(0,4)])
arr_copy=arr.copy()
print(arr_copy)

Array slicing does no copy corresponding elements of the array, rather it creates a view of the array, which may be helpful in certain circumstances and may not be helpful in some other situations, thus, to copy an array or some portion of the array we need to use the copy() function as shown above.

6. Give an example of how will you reshape an array of 2-dimension into 3-dimensions?

Ans:-

import numpy as np
arr=np.array([[1,2,3,4] for i in range(0,4)])
print(arr)
arr_new=arr.reshape((2,2,4))
print(arr_new)

reshape() function can be used to change the shape of an already existing NumPy array.

7. Give a method other than reshape to add a new axis to the array?

Ans:- Using np.newaxis keyword.

import numpy as np
arr=np.array([[1,2,3,4] for i in range(0,4)])
print(arr)
arr_new=arr[np.newaxis,:,:]
print(arr_new)

np.newaxis ,adds a new axis to the element around which it is applied.
In the above example, arr will be [[1,2,3,4],[1,2,3,4],[1,2,3,4],[1,2,3,4]], having shape of(4,4) and after using new_axis it will create a new_axis at the outermost level and arr_new will be [[[1,2,3,4],[1,2,3,4],[1,2,3,4],[1,2,3,4]]], having shape of (1,4,4).

8. Give a method to concatenate three NumPy arrays?

Ans:-

x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
z = np.array([4, 5, 6])
np.concatenate([x, y,z])

np.concatenate() function can be used to concatenate any number of arrays at once, given all the input arrays have the same number of dimensions, in this case 1.

9. Give an example to split an array into three arrays?

Ans:-

x = [1, 2, 3, 99, 99, 3, 2, 1]
x1, x2, x3 = np.split(x, [3, 5])
print(x1, x2, x3)

np.split() function can be used to split an array into n subarrays using the format shown above in the code.

10. Use appropriate NumPy ufunc to calculate the absolute value of a NumPy array?

Ans:-

x = np.array([3 + 4j, 4 + 3j, 2 - 0j, 0 - 1j])
np.abs(x)

np.abs() is an alias for np.absolute(), and hence. both could have been used here interchangeably.

11. Calculate the logarithm of an array(base should be 10)?

Ans:-

x = [1, 2, 4, 10]
print("log10x =", np.log10(x))

np.log10(x) will result in an array consisting of the logarithm to the base 10 for each element in the array.

12. What is the difference between np.log1p(array_name) and np.log(array_name)?

Ans:-

When values in the array are very small then np.log1p(array_name) would give more precise value than that given by np.log(array_name).

13. Give a method showing how to apply reduce method for binary ufuncs ?

Ans:-

x = np.arange( 6)
np.add.reduce(x)

np.add function can only be used to calculate sum of two arrays element-by-element, while using reduce we can make it work upon a single array, and it is true for any binary ufunc.

14. Give a way to store all the intermediate results of the computation performed by reduce method?

Ans:-

x = np.arange( 6)
np.add.reduce(x)
np.add.accumulate(x)

x will be an array([0,1,2,3,4,5]), np.add is used to add two arrays ,but to make it perform over a single array we use reduce method, which takes an array and performs whatever operation to which it has been applied by taking two elements at once and replacing the two elements with the result and then again doing the same thing till only a single element remains, thus np.add.reduce(x) will add all the elements of the array and will result in its value namely 15, while np.add.accumulate keeps a track of the element at the beginning of the array over which reduce method has been applied, till that array contains only a single element, and thus it results an array containing values of the function over which accumulate function(in this case add) is applied for every operation.
array([ 0, 1, 3, 6, 10, 15]) will be the output of the np.add.accumulate(x).

15. Give an example showing braodcasting ?

Ans:-

a = np.array([0, 1, 2])
b = np.array([5])
a+b

Here, array b has been broadcasted to match the shape of array a.
Earlier it has shape of (1,1), which can be extended to match the shape of a which is (1,3), thus, array b would become array([5,5,5]), and a+b can now happen without any concern with output array([5,6,7]).
We are going to see the rules of broadcasting later in this interview preparation sheet.

16. Give an example showing comparison operators over the NumPy array?

Ans:-

x = np.array([1, 2, 3, 4, 5])
x < 3

Its output would be array([True, True, False, False, False, False]),
as any relational operator applied over a numpy array results in a boolean array with True being the value for elements qualifying the condition while False being the value for condition being false.
All six of standard comparison operations can be applied which are <,>,<=,>=,==,!=.

17. Using np.sum calculate the number of elements lesser than a particular value ?

Ans:-

x=np.array([[5 0 3 3]
   [7 9 3 5]
   [2 4 7 6]])
np.sum(x < 6)

Firstly we have initialized the numpy array x, then suppose we have to count the numbers lesser than a particular value thus, we use x<6 to create a boolean array, and since True is interpreted as 1, and a False as 0, we simply input the boolean array into the np.sum() to get the count of the elements lesser than a particular value in the array.

18. What is the equivalent ufuncs for bitwise Boolean operators(&,|,^,~)?

Ans:-

Corresponding ufuncs for bitwise Boolean operators are:-
& - np.bitwise_and
| - np.bitwise_or
^ - np.bitwise_xor
~ - np.bitwise_not

19. Give a simple code showing the use of fancy indexing in the code?

Ans:-

x=[23,43,45,67,65,89,90]
index=[2,4,6]
x[index]

Its output will be elements at corresponding position, array([45,65,90]).

20. Show an example of modification using fancy indexing?

Ans:-

x = np.arange(12)
i = np.array([1, 3, 9, 4])
x[i] = 12

Here, elements with corresponding indices will be modified to 12.

21. Which sorting algorithm does NumPy's np.sort uses and what is its time complexity?

Ans:-

np.sort uses an O( N log N) , quick‐sort algorithm.

22. Give an example which outputs the original index of elements in the sorted array?

Ans:-

x = np.array([2, 1, 4, 3, 5])
i = np.argsort(x)

Here, np.argsort is used to return the index of the sorted values in the original array.

23. Give an example initializing a NumPy array with structured data?

Ans:-

name = ['Apple', 'Mango', 'Carrot']
id = [25, 45, 37]
weight = [55.0, 85.5, 68.0]
data = np.zeros(3, dtype={'names':('name', 'id', 'weight'),
'formats':('U10', 'i4', 'f8')})
data['name'] = name
data['age'] = age
data['weight'] = weight
print(data)

Structured array can be used to store and manipulate record like arrays, and can be initialised like the way shown above.
dtype.names store the field names and dtype.formats store their data type.
There are several other ways to create a structured array, which can be seen in NumPy documentation.

24. Show the use of np.recarray class and explain its usage?

Ans:-

data_rec = data.view(np.recarray)
data_rec.age

Here, we are in the continuation of 28th question and using data to be same in 29th question as well.
Basically, using np.recarray class, the fields can be accessed as
attributes rather than as dictionary keys as we have done in the above lines of code as opposed to data['age'].

25. Perform matrix multiplication between two arrays?

Ans:-

x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
np.dot(x, y)

Simply, doing x* y would result in multiplication of corresponding elements of the matrix, therefore to do matrix multiplication np.dot(array_a,array_b) is used, where array_a and array_b are numpy arrays and they must be compatible for this operation, otherwise it will throw an error.

Predict the output:-

1. Give the output of the following code:-

x=[[23,43],[45,67],[65,89]] 
x[2,[0,1]]?

Ans:-

It will be array([65,89]), using fancy indexing, 2 will combine with both 0 and 1 to give both x[2][0] and x[2][1] as the output.

2. Give the output of the following code:-

x=[1,2,3,4,5]
x[x<5]?

Ans:-

It will be array([1,2,3,4]), as x<5 will return a boolean array([True,True,True,True,False]), and x[array([True,True,True,True,False]), returns the elements for the indices where boolean value is true ,this, we get array([1,2,3,4]).

3. Give the output of given lines of code?

a = np.arange(3)
b = np.arange(3)[:, np.newaxis]
print(a)
print(b)
print(a+b)

Ans:-

array([0,1,2])
array([[0],[1],[2]])
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])
Here, a = np.arange(3) results in array([0,1,2]), b = np.arange(3) will result in array([0,1,2]) and therefore, b = np.arange(3)[:,np.newaxis] will result in array([[0],[1],[2]]), as a new axis will be added for each element of array.
As dimensions of array a is(1,3), and array b is (3,1), thus, broadcasting rules are applied ,and thus, a will be of the shape (3,3) and it will be equal to array([[0,1,2],[0,1,2],[0,1,2]]), similarly, b has shape of (3,1) and it will be broadcasted to array([[0,0,0],[1,1,1],[2,2,2]]), now, there shapes are same and can be added resulting in array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]]).

4. Give the output:-

a=np.array([[ 0.8967576 0.03783739 0.75952519 0.06682827]
            [ 0.8354065 0.99196818 0.19544769 0.43447084]
            [ 0.66859307 0.15038721 0.37911423 0.6687194 ]])?
array_name.max(axis=1)

Ans:-

It will be array([0.8967576 , 0.99196818 , 0.75952519 , 0.6687194]).
As axis=1 will be the innermost axis, and thus first element will be max([0.8967576 0.8354065 0.66859307], second element will be max([0.03783739
0.99196818 0.15038721]) , third element will be max([0.75952519 0.19544769 0.37911423]), fourth element will be max([0.06682827 0.43447084 0.6687194]).
That is, all those elements where axis 1's values are same, they are clubbed together and then maximum among them is found.
Like here, a[0][0],a[1][0],a[2][0] are clubbed together, similarly, a[0][1],a[1][1],a[2][1] are clubbed together, a[0][2],a[1][2],a[2][2] are clubbed together, and a[0][3],a[1][3],a[2][3] are clubbed together.
Same is the case for any other axis , you just need to find out which axis needs to be fixed, axis =0 is always the outermost axis, and as we go inwards its value increases by 1, thus in a 3-D array axis=1 will be the middle one and axis =2 will be the innermost axis.

5. Give the output:-

np.arange(4)/np.arange(1,5)?

Ans:-

Output will be array([0 , 0.5 , 0.6666667 , 0.75].
As np.arange results in array([0,1,2,3]), and np.arange([1,5]), would result in array([1,2,3,4]), and using principles of vectorization and if needed and possible broadcasting every corresponding element of both arrays is divided and thus, resulting in the output array.

6. Give the output:-

dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr

Ans:-

Output will be:-
array([([0, 0, 0], 0), ([0, 0, 0], 0), ([0, 0, 0], 0), ([0, 0, 0], 0)],dtype=[('x', '<i8', (3,)), ('y', '<i4')])
As above method is yet another method to create a structured array, since, in dtype, size of x is 3, thus, an array of 3 0's are created, and another element y of int32 data type. Thus, each row containing an array of 3 elements and a single integer.

7. Give the output:-

values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer

Ans:-

Output will be:-
array([1, 2, 4, 3, 0])
argsort function returns the index of the sorted elements in the original array.
Original array is [5,0,1,3,2] which after sorting gets converted to [0,1,2,3,5] and thus values.argsort becomes[1,2,4,3,0] indices of sorted array elements in the original array.

8. Give the output:-

arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)

Ans:-

Its output will be 3.
searchsorted is a function that performs a binary search on a sorted array,
returning the location in the array where the value would need to be inserted to maintain sortedness. You may also insert array of values to get array of indices where those values need to be inserted to keep the sortedness.

9. Give the output:-

arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]

Ans:-

Output:-
array([[0,1],[2,3],[4,5],[.1383,.0983],[1.234,4.332],[-0.1234,9.4109]]).
np.r_ is used to stack elements of two arrays row-wise. Similarly, np.c_ is used to stack it column wise.

10. Give the output:-

ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
np.unique(ints)

Output:-
array([1,2,3,4]).
There are various set logic which can be applied over a NumPy array as is shown above where it returns the unique values in the array.

Some set logics which can be used over a NumPy array is shown below:-
unique(x):-
Compute the sorted, unique elements in x
intersect1d(x, y):-
Compute the sorted, common elements in x and y
union1d(x, y):-
Compute the sorted union of elements
in1d(x, y):-
Compute a boolean array indicating whether each element of x is contained in y
setdiff1d(x, y):-
Set difference, elements in x that are not in y
setxor1d(x, y):-
Set symmetric differences; elements that are in either of the arrays, but not both

11. Give the output:-

arr =np.array( [[[ 0, 1, 2, 3],
        [ 4, 5, 6, 7]],
        [[ 8, 9, 10, 11],
        [12, 13, 14, 15]]])
arr.swapaxes(1, 2)

Ans:-

Output will be :-
array([[[ 0, 4],
[ 1, 5],
[ 2, 6],
[ 3, 7]],
[[ 8, 12],
[ 9, 13],
[10, 14],
[11, 15]]])
As axes 1st and 2nd would be interchanged, it can be most easily understood by checking the shape of two arrays , the original array's shape was (2,2,4), and the swapped array has the shape of (2,4,2).

12. Give the output:-

arr = np.array([[1., 2., 3.], [4., 5., 6.]])
arr2= np.array([[0 , 4 , 1 ], [7 ,10 ,12 ]])
arr > arr2

Ans:-

Output will be :-
array([[False, True, False],[ True, False, True]], dtype=bool).
It simply compares corresponding elements of the array and converts it into a boolean array of the same shape and size.

13. Give the output:-

x = [1, 2, 3]
np.exp2(x)

Ans:-

Output will be :-
array([ 2. 4. 8.]).
It simply results in value 2^x for every element of x, similarly you can think of the function to calculate the value of 3^x intuitively to be exp3(x), and for n^x to be expn(x), where n is an integer.

14. Give the output:-

x=np.array([ 6. 0. 0. 0. 0. 0. 0. 0. 0. 0.])
i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x

Ans:-

Output will be :-
array([ 6., 0., 1., 1., 1., 0., 0., 0., 0., 0.]).
You might expect that x[3] would contain the value 2, and x[4] would contain the value 3, as this is how many times each index is repeated. Conceptually, this is because x[i] += 1 is meant as a shorthand of x[i] = x[i] + 1 .
x[i] + 1 is evaluated, and then the result is assigned to the indices in x . It is not the augmentation that happens multiple times, but the assignment,
which leads to the rather nonintuitive results
And the same is the case with any other operation of similar type, thus, remember it is the assignment not the augmentation, but what if we want another behaviour where we want operation to be performed at every index?
We are going to see it in the below example.

15. Give the output:-

x=np.array([ 6. 0. 0. 0. 0. 0. 0. 0. 0. 0.])
np.add.at(x, i, 1)
print(x)

Ans:-

Output will be:-
array([ 6., 0., 1., 2., 3., 0., 0., 0., 0., 0.]).
The at() method does an in-place application of the given operator at the specified indices. It bascialle translates to doing x[i]=x[i]+1, at every indices not withstanding whether it has been applied at the same index earlier or not.

Descriptive questions:-

1. What are the advantages of using NumPy?

Ans:-

It helps in reducing loops, and thus, making our code more cleaner and readable.Also, since, it uses algorithms written in C, thus, its speed is much faster than that of the code written in standard Python doing the same operations. Thus, in short, clearer code, lesser loops and faster speed are the advantages of using NumPy.

2. How is a NumPy array different from a Python list?

Ans:-

To know the differences between them, firstly we need to see the differences between C and Python as NumPy is implemented in C.
C is a statically typed language while NumPy is dynamically types, which means data types in C are explicitly stated while in the case of Python they are inferred, which causes delayed execution or time-consuming execution. Standard Python implementation is just a cleverly disguised C structure, which contains not only its value but also some extra information as well, and a Python variable is a pointer to a position in memory containing all the Python object information while C's variable is essentially a label for a position in a memory whose bytes encode a value according to the data type explicitly stated.
Because of this property we can create heterogeneous lists in Python which is not the case in C. At the implementation level, the array(in C) essentially contains a single pointer to one contiguous block of data. The Python list, on the other hand, contains a pointer to a block of pointers, each of which in turn points to a full Python object like the Python
integer(or any other different object like string,etc). Again, the advantage of the list is flexibility: because each list
element is a full structure containing both data and type information, the list can be filled with data of any desired type. Fixed-type NumPy-style arrays lack this flexibility, but are much more efficient for storing and manipulating data.

3. What extra information does a Python variable contains?

Ans:-

struct _longobject {
long ob_refcnt;
PyTypeObject *ob_type;
size_t ob_size;
long ob_digit[1];
};

Above given snippet is the structure for integer variables in Python, as you can see it does not only contain its value, but also a lot of extra information to make it dynamically types which are responsible for the flexibility of Python, but at the expense of causing some delay.

4. Write all NumPy standard Data Types?

Ans:-

bool_ :- Boolean (True or False) stored as a byte
int_ :-Default integer type (same as C long ; normally either int64 or int32 )
intc :-Identical to C int (normally int32 or int64 )
intp :-Integer used for indexing (same as C ssize_t ; normally either int32 or int64 )
int8 :-Byte (–128 to 127)
int16 :-Integer (–32768 to 32767)
int32 :-Integer (–2147483648 to 2147483647)
int64 :-Integer (–9223372036854775808 to 9223372036854775807)
uint8 :-Unsigned integer (0 to 255)
uint16 :-Unsigned integer (0 to 65535)
uint32 :-Unsigned integer (0 to 4294967295)
uint64 :-Unsigned integer (0 to 18446744073709551615)
float_ :-Shorthand for float64
float16 :-Half-precision float: sign bit, 5 bits exponent, 10 bits mantissa
float32 :-Single-precision float: sign bit, 8 bits exponent, 23 bits mantissa
float64 :-Double-precision float: sign bit, 11 bits exponent, 52 bits mantissa
complex_ :-Shorthand for complex128
complex64 :-Complex number, represented by two 32-bit floats
complex128 :-Complex number, represented by two 64-bit floats

5 What is vectorization?

Ans:-

It is the process in which same operation is performed for each element in the array, thus, removing the loops ,making our codes faster and more readable.

6. What are NumPy UFuncs?

Ans:-

Since, Python loops are sluggish due to the dynamically typed nature of Python, small operations when done repeatedly make our program really slow, to solve this bottleneck and to counter the bad effects of dynamically typed feature at the expense of loss of heterogeneousity in array, NumPy provides a convenient interface into this kind of statically typed, compile routine, which is known as vectorized operation, we can accomplish this by simply performing an operation on the array, for which it supplies us with unary ufuncs or binary ufuncs, to accomplish the operation. This vectorized approach combined with ufunc is designed to push loop into the compiled layer that underlies NumPy, leading to much faster execution.

7. What is Broadcasting?

Ans:-

Broadcasting is simply a set of rules for applying binary ufuncs on arrays of different shapes and sizes.
For e.g.:-

a=np.array([1,2,3,4,5])
print(a+5)

would result in an array([6,7,8,9,10]), thus broadcasting our scalar number into an array([5,5,5,5,5]).
NumPy automatically broadcasts two arrays wherever it is possible according to the rules of broadcasting.

8. What are the rules of broadcasting?

Ans:-

"1:- If the two arrays differ in their number of dimensions, the shape of the one with fewer dimensions is padded with ones on its leading (left) side.
2:- If the shape of the two arrays does not match in any dimension, the array with shape equal to 1 in that dimension is stretched to match the other shape.
3:- If in any dimension the sizes disagree and neither is equal to 1, an error is raised."

9. What is the difference between keywords and/or versus Operators &/| which you may encounter while applying Boolean operations on the NumPy array?

Ans:-

The difference is that 'and' and 'or' gauge the truthness of an entire object while '&' and '|' refer to bits within each object.
For e.g.:-

A = np.array([1, 0, 1, 0, 1, 0], dtype=bool)
B = np.array([1, 1, 1, 0, 1, 1], dtype=bool)
A | B

would result in array([True,True,True,False,True,True], dtype=bool)

while A or B would result in an error as it would try to find the truthness of two arrays which is not defined.
So remember this: 'and' and 'or' perform a single Boolean evaluation on an entire object, while '&' and '|' perform multiple Boolean evaluations on the content (the individual bits or bytes) of an object.

10. What is structured Data in NumPy?

Ans:-

We learned that array items all have to be the same data type, but that wasn’t entirely correct. NumPy has a special kind of array, called a record array or structured array, with which you can specify a type and, optionally, a name on a per-column basis, and it can feel similar to working with data in Excel, CSVs, or relational databases.

Some Practical Coding Examples:-

1. Implement a chess board pattern on an 8 by 8 array , use 1 for black squares and 1 for white squares?

Ans:-

a=np.zeros([8,8])
a[1::2,0::2]=1
a[0::2,1::2]=1
print(a)

Output:-

2. Find the necessary statistical measures of the given array consisting of the heights of random people:-

[189 170 189 163 183 171 185 168 173 183 173 173 175 178 183 193 178 173 174 183 183 168 170 178 182 180 183 178 182 188 175 179 183 193 182 183 177 185 188 188 182 185]

Ans:-

data=np.array([189, 170, 189, 163, 183, 171, 185, 168, 173, 183, 173, 173, 175, 178, 183, 193, 178, 173, 174, 183, 183, 168, 170, 178, 182, 180, 183, 178, 182, 188, 175, 179, 183, 193, 182, 183, 177, 185, 188, 188, 182, 185])
print("Mean height:", data.mean())
print("Standard deviation", data.std())
print("Minimum height:", data.min())
print("Maximum height:", data.max())
print("25th percentile:",np.percentile(data,25))
print("Median:",np.median(data))
print("75th percentile:", np.percentile(data,75))

Output:-

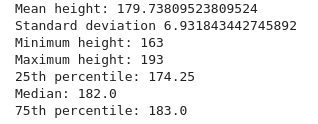
All the above functions are NumPy functions to calculate basic statistical measures.

3. Create a multiplication table till 10 using NumPy.

Ans:-

x = np.arange(1, 11)
np.multiply.outer(x, x)

Output:-

outer function is used to apply the operation for every two possible values of the array.

4. Calculate the value of 3* e^3 using the corresponding sequence of z* e^z by implementing it in NumPy?

Ans:-

from math import e, factorial
import numpy as np
fac = np.vectorize(factorial)
def x_e_x(x, terms=10):
    n = np.arange(terms)
    return np.sum(n*(x ** n) / fac(n))
if __name__ == "__main__":
    print("Actual:", 3*e ** 3)  # Using e from the standard library
    print("N (terms)\tMac\tError")
    for n in range(1, 14):
        mac = x_e_x(3, terms=n)
        print(f"{n}\t\t{mac:.03f}\t\t{3*e**3 - mac:.03f}")

Output:-

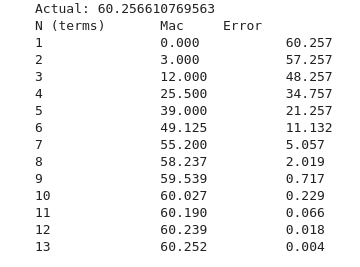
Above code is a way to find out the value of z * e^z using its corresponding series. We have used NumPy to show that it eliminates the necessity of loop in these types of code and is easier to follow like a mathematical equation.

5. Implement a one dimensional random walk of 1000 steps .

Ans:-

import matplotlib.pyplot as plt
no_of_steps = 1000
draws = np.random.randint(0, 2, size=no_of_steps)# drawing random integers 0 or 1.
steps = np.where(draws > 0, 1, -1)# if 0 is drawn then move -1 else +1.
walk = steps.cumsum() # random walk is position reached after the end of ceratin no_of_seps which in this case is 1000.
plt.plot(walk[:1000])# matplotlib functions to plot 
plt.show()# matplotlib function to show the created plot object

We can only visualise this for which we may have to use matplotlib library.

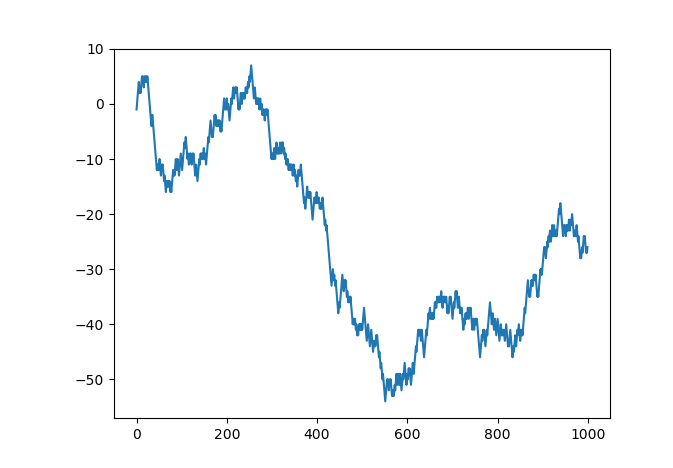
Here, we have tried to list out questions from all the relevant sections of NumPy to help you revise it once before appearing for the interview.
Hoping, it would be helpful for you .
Cheers, and All The Best for your interviews.