
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored an insightful approach/ algorithm to find the number of interior integral points of a rectangle. This is an important concept in the field of computational geometry.
TABLE OF CONTENTS
- Problem Statement Definition
- Intuition
- Pick's Theorem
- Mathematical Formulation
- Solution Analysis
- Area of a randomly-oriented rectangle
- Integral points on a line segment
- Naive approach
- Optimized approach
- Algorithm
- Implementation
- Python
- C++
- Time-Complexity analysis
- Space-Complexity analysis
- Applications
Reading time: 25 minutes | Coding time: 15 minutes
Prerequisites:
Let us dive right into the solution!
1) PROBLEM STATEMENT DEFINITION
To put the problem in simpler words- We are given the x and y coordinates of the four vertices of a rectangle. We need to find the number of integral coordinates inside the rectangle.
Let us understand this with an example:
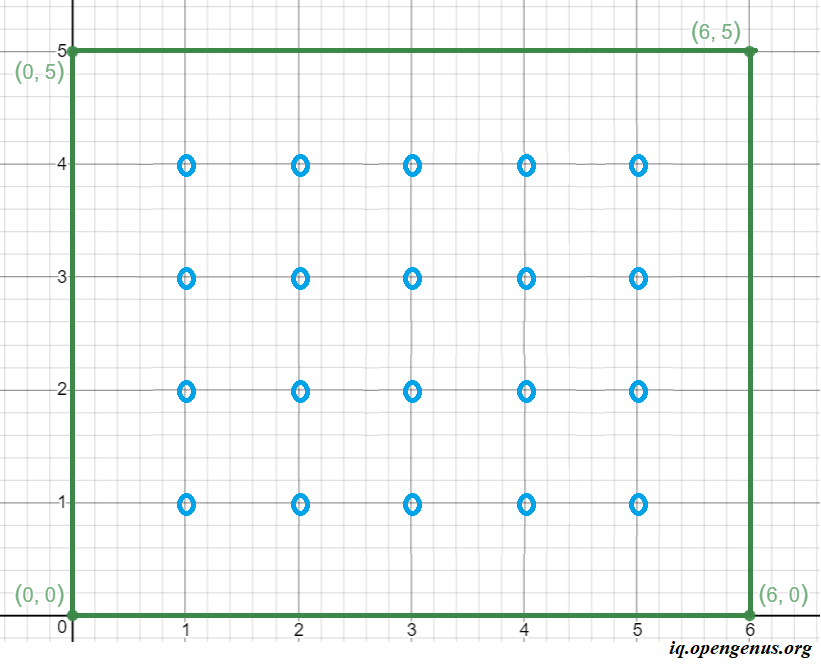
Suppose we have are given the cooridinates as (0,0) , (6,0), (0,5) and (6,5). Let us plot the points.
Let us construct the rectangle:
Now, let us plot the interior integral coordinates,
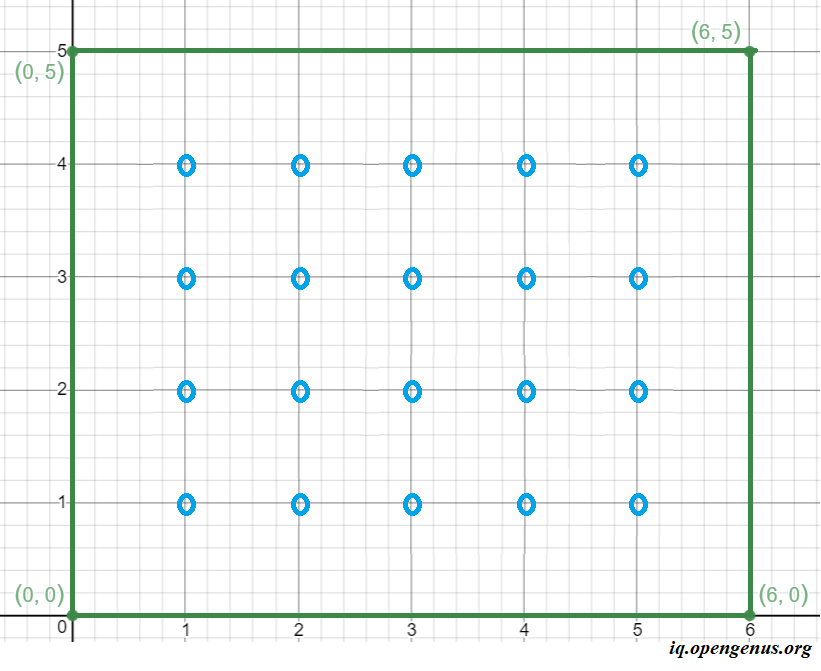
Thus, we can plot 20 interior points which are integers. Thus the solution for the points: (0,0) , (6,0), (0,5) and (6,5) is 20.
2) INTUITION
It seems easy to find the interior integral points of a rectangle parallel to the X axis, like in the example. It seems like it is just (length-1) * (breadth-1)
but it is intuitively, not an easy task to implement a program to calculate the interior integral points inside a randomly-oriented rectangle like the example below. There are no naive methods for solving this problem.
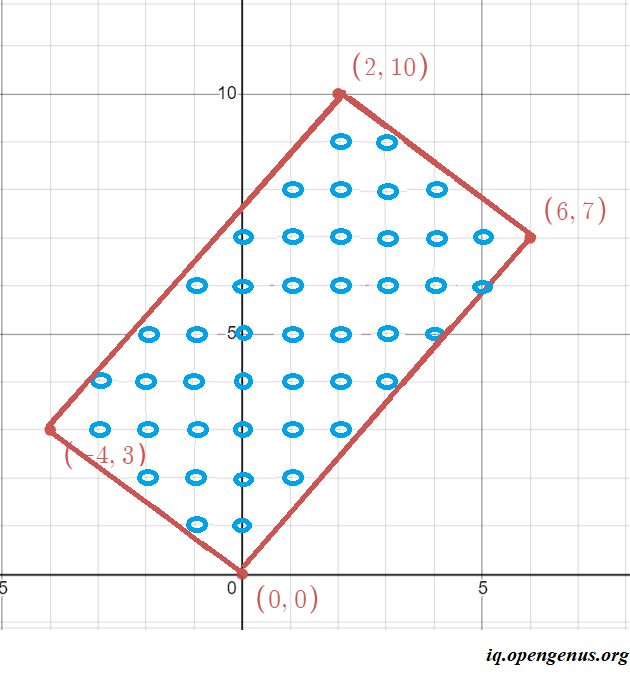
In the above example the length of the rectangle is 9.22 and the breadth is 5 and by out approach the number of interior integral points must either be (4 * 9 = 36) or (4 * 10 = 40) because of the uncertainty with decimals. But the answer is 45.
If only there was a simple formula that could easily give us the answer we are looking for!
3) PICK'S THEOREM
Austrian mathematician Georg Alexander Pick, in 1899, gave us a formula to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.
For any general polygon, Pick's theorem provides a way to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.
Since a rectangle is a polygon, the formula can be applied for our problem statement.
3.1) Mathematical Formulation
We are given a certain rectangle with non-zero area. We denote its area by A, the number of points with integer coordinates lying strictly inside the rectangle by I and the number of points lying on polygon sides by B.
Thus, the Pick's formula states that:
i.e, Area of a rectangle = (Integral interior points)+((Integral points on the edges)/2)−1
A = I + B/2 -1
You can go through the proof for the theorem here
4) SOLUTION ANALYSIS (identifying sub-problems)
From pick's theorem, we can deduce that the number of interior integral points
I = (2A - B + 2) / 2.
Thus the two sub-problems are to find the:
- Area of the randomly-oriented rectangle
- Number of interior integral points
Let us find their optimal solutions!
4.1) Area of a randomly-oriented rectangle
This is a standard middle school formula: area = length * breadth.
And the length of line segment between two given points (x1,y1) and (x2,y2) is root( (x2-x1)^2 + (y2-y1)^2 )
But the problem lies in finding the length and breadth. Since we are given only the coordinates, The problem lies in selecting the 2 coordinates for finding either the length or breadth because the user might enter the points in any order.
For example in the example below:
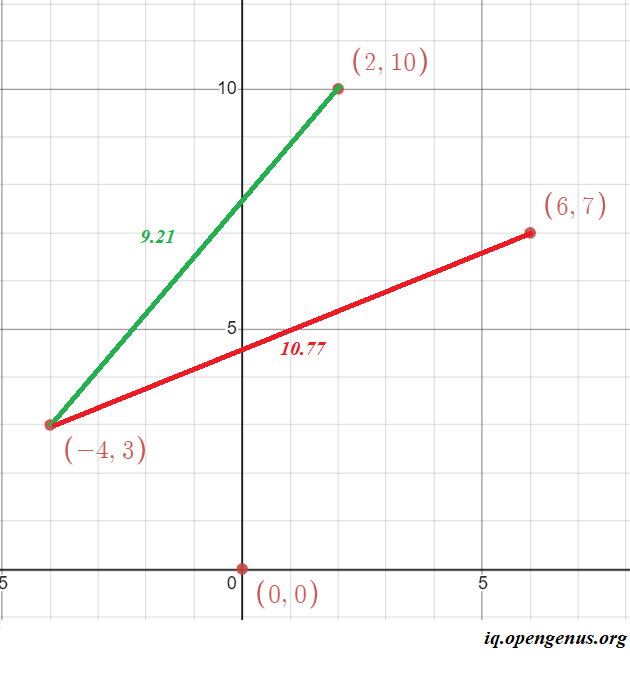
if we consider the points (-4,3) and (2,10) we get a length of 9.21, else if we consider the points (-4,3) and (6,7) we get a length of 10.77
Thus we must develop an algorithm to give us the correct length and breadth irrespective of the order of input.
The simplest idea is to fix one point and find its distance with all other points. The maximum length is the diagonal, so it is discarded. The least distance is the breadth and the remaining distance is the length.
The psuedocode for it is as follows:
double lendth_breadth(){
double d1 = sqrt(pow( (x2-x1), 2) + pow( (y2-y1), 2));
double d2 = sqrt(pow( (x3-x2), 2) + pow( (y3-y2), 2));
int d3 = sqrt(pow( (x1-x3), 2) + pow( (y1-y3), 2));
breadth = min( d1, min(d2, d3)) ;
double diagnol = max( d1, max(d2, d3)) ;
length = d1+ d2+ d3 - breadth - diagnol;
}
4.2) Number of integral points on the edges of the rectangle
Let us reduce the problem to Number of integral points on a line. To understand, let us take an example. Consider two points (-1,4) and (6,4). Let us plot the points.
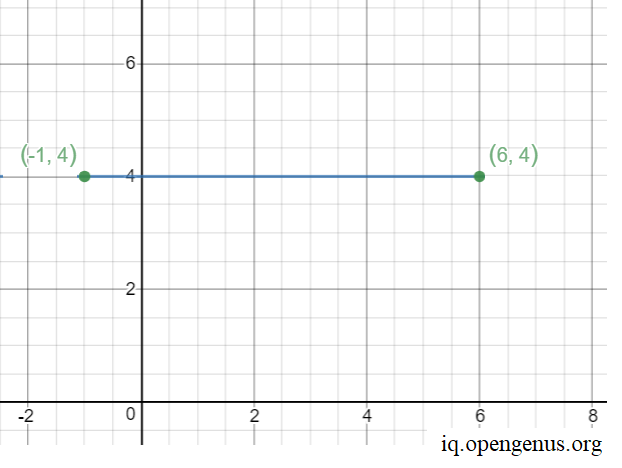
Let us visually note and plot the integral points on the line.
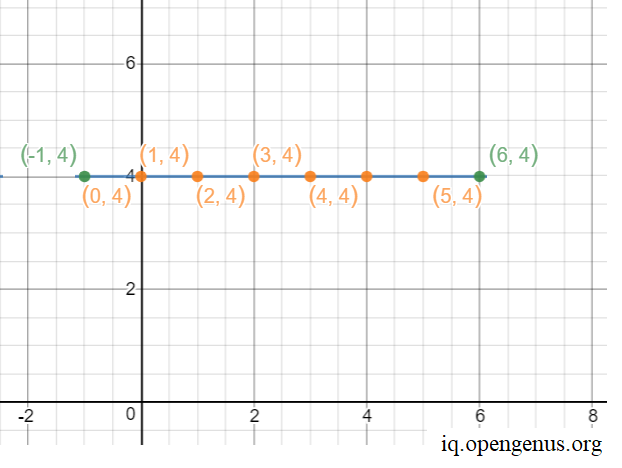
Thus, there are 6 points on the line.
To solve this sub-problem, here are two approaches.
4.2.1) Naive approach
- Read the input of two points.
- Initialize a count variable to zero.
- Consider any one of the two given points.
- Reach the other end point by using a loop incrementing by 1.
- For every point inside the loop, check if it lies on the line that joins given two points.
- If yes, then increment the count by 1.
4.2.2) Optimized (GCD) approach
The line can be divided into one of three distinct categories
- If edge is parallel to the Y-axis, then the number of integral points in between is : abs(p.x - q.x)-1
- If the edge formed by joining p and q is parallel to the X-axis, then the number of integral points between the vertices is : abs(p.y - q.y)-1
- Else, we can find the integral points between the vertices using below formula: GCD(abs(p.x - q.x), abs(p.y - q.y)) - 1
The above formula is a well known and can be proved using simple geometry. This approach works on the idea that shifting the edge such that one of the vertex lies at the origin does not change the characteristics that make the calculation of its intgral points.
In other words, it is easier to calculate the answer when coefficients a, b and c in the equation:
ax + by +c = 0 become co-prime. This can be achieved by calculating the GCD (greatest common divisor) of a, b and c. This converts the coefficients to the simplest form.Then, the answer will be y2-y1/(a-1) because after calculating ax + by + c = 0, for different y values, x will be number of y values which are exactly divisible by a.
Below is the psuedocode for this approach.
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a%b);
}
int getCount(Point p, Point q)
{
if (p.x==q.x)
return abs(p.y - q.y) - 1;
if (p.y == q.y)
return abs(p.x-q.x) - 1;
return gcd(abs(p.x-q.x), abs(p.y-q.y))-1;
}
Now that we have identified the sub-problems and their optimal solutions, let us move onto the bigger picture - finding the number of Integral points inside a rectangle using pick's formula.
5) ALGORITHM
- Read the input points as three sets of x and y coordinates (namely x1,y1 , x2,y2, x3,y3 and x4,y4)
- Find the length and breadth by calling the length_breadth function as described above
- Find the area of the traingle by multiplying length and breadth.
- Find the number of integral points on the four line-segments connecting the vertices using the algorithm mentioned above and intialize it to B.
- Find the number of interior integral points (I) by applying the formula mentioned above.
6) IMPLEMENTATION
- Python code:
import math
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def gcd(a, b):
if (b == 0):
return a
return gcd(b, a % b)
def Integral_points_on_line(p, q):
if (p.x == q.x):
return abs(p.y - q.y) - 1
if (p.y == q.y):
return abs(p.x - q.x) - 1
return gcd(abs(p.x - q.x),
abs(p.y - q.y)) - 1
def area(p, q, r ,s):
d1 = sqrt(pow( (x2-x1), 2) + pow( (y2-y1), 2));
d2 = sqrt(pow( (x3-x2), 2) + pow( (y3-y2), 2));
d3 = sqrt(pow( (x1-x3), 2) + pow( (y1-y3), 2));
breadth = min( d1, min(d2, d3)) ;
diagnol = max( d1, max(d2, d3)) ;
length = d1+ d2+ d3 - breadth - diagnol;
return (breadth * length)
def Integral_interior_points(p, q, r):
BoundaryPoints = (Integral_points_on_line(p, q) + Integral_points_on_line(q, r) + Integral_points_on_line(r, s) + Integral_points_on_line(s, q) + 12)
return (math.floor((2*area(p, q, r, s) - BoundaryPoints + 2)/2))
if __name__=="__main__":
p = Point(-4, 3)
q = Point(6, 7)
r = Point(0, 0)
s = Point(2, 10)
print("Number of integral points inside given rectangle is ", Integral_interior_points(p, q, r ,s))
2.C++ code:
#include <iostream>
#include <cmath>
#include<algorithm>
using namespace std;
double length, breadth;
struct Point
{
int x;
int y;
};
void lendth_breadth(Point p, Point q, Point r, Point s){
double d1 = sqrt(pow( (q.x-p.x), 2) + pow( (q.y-p.y), 2));
double d2 = sqrt(pow( (r.x-p.x), 2) + pow( (r.y-p.y), 2));
double d3 = sqrt(pow( (s.x-p.x), 2) + pow( (s.y-p.y), 2));
breadth = min( d1, min(d2, d3)) ;
double diagnol = max( d1, max(d2, d3)) ;
length = d1+ d2+ d3 - breadth - diagnol;
}
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a%b);
}
int Integral_points_on_line(Point p,Point q)
{
if (p.x==q.x)
return abs(p.y - q.y) - 1;
if (p.y == q.y)
return abs(p.x - q.x) - 1;
return gcd(abs(p.x-q.x), abs(p.y-q.y)) - 1;
}
int Integral_interior_points(Point p, Point q, Point r, Point s)
{
int BoundaryPoints = Integral_points_on_line(p, q) + Integral_points_on_line(q, r) + Integral_points_on_line(r, s) + Integral_points_on_line(s, p) + 12;
lendth_breadth(p, q, r, s);
int d_Area = floor(2 * length * breadth);
return (d_Area - BoundaryPoints + 2)/2;
}
int main()
{
Point p,q,r,s;
p.x=0;
p.y=0;
q.x=6;
q.y=0;
r.x=0;
r.y=5;
s.x=6;
s.y=5;
cout << "Number of integral points inside given rectangle is "<< Integral_interior_points(p, q, r, s);
return 0;
}
OUTPUT:
Number of integral points inside given rectangle is 20
The solution given by the program is:
7) TIME COMPLEXITY ANALYSIS
The time-complexity of GCD algorithm is O(loga)+O(logb) if we are finding the GCD of a and b.
Finding the integral points on the edges runs in constant time.
Substituting the values in Pick's formula and finding the Number of integral points inside the given rectangle also takes constant time.
Hence, the driver of the overall time-complexity is GCD in the worst and average case but in the best case scenario, the points may be arranged in such a way that GCD function is not used
- Worst case time complexity:
Θ(2* (log n) ), when a=b=n or b=c=n or c=a=n and n is large - Average case time complexity:
Θ(log n), when a,b and c are consecutive Fibonacci numbers - Best case time complexity:
Θ(1),when either the GCD function is not called or a is a multiple of b and b is a multiple of c, then Euclid GCD terminates in one call.
8) SPACE-COMPLEXITY ANALYSIS
The algorithm proposed does not use auxiliary space. Since, we do not use any extra space, the space complexity is Θ(1)
9) APPLICATIONS
- An extension of this algorithm is used by online battleships engine.
- An extension of this algorithm is used to calculate the pixels in a particular portion of a picture. This is done by dividing the portion with similar colour intensity into rectangles or squares.
- It is used used in other computational geometry problems.
10) TEST YOUR UNDERSTANDING
The algorithm can be divided into sub-problems of 1. GCD 2. Pick's formula 3. Integral points on a line 4. Area of the rectangle Intuitively, what is the order of execution of the steps in the algorithm?With this article at OpenGenus, you must have the complete idea of Finding the Number of Integral points inside a rectangle!.
