
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be discussing Time and Space Complexity of most commonly used binary tree operations like insert, search and delete for worst, best and average case.
Table of contents:
- Introduction to Binary Tree
- Introduction to Time and Space Complexity
- Insert operation in Binary Tree
- Worst Case Time Complexity of Insertion
- Best Case Time Complexity of Insertion
- Average Case Time Complexity of Insertion
- Searching / Find Operation
- Worst Case Time Complexity of Search
- Best Case Time Complexity of Search
- Average Case Time Complexity of Search
- Deletion Operation
- Worst Case Time Complexity of Delete
- Average Case Time Complexity of Delete
- Best Case Time Complexity of Delete
- Space Complexity of Insert, Search and Delete
- Conclusion
Prerequisites:
This is the summary which you will understand once you go through this article:
Time Complexity of different operations in Binary Tree:
| Operation | Worst Case | Average Case | Best Case |
|---|---|---|---|
| Insert | O(N) | O(N0.5) | O(logN) |
| Search | O(N) | O(N0.5) | O(1) |
| Delete | O(N) | O(N0.5) | O(logN) |
Space Complexity of different operations in Binary Tree:
| Operation | Iterative | Recursive, average |
|---|---|---|
| Insert | O(1) | O(H) = O(N0.5) |
| Search | O(1) | O(H) = O(N0.5) |
| Delete | O(1) | O(H) = O(N0.5) |
where N = number of nodes in Binary Tree, H = height of Binary Tree
Introduction to Binary Tree
A Tree Data Structure represents a hierarchical tree structure , with a root value and subtrees of children with a parent node , represented as a set of linked nodes.
A Binary Tree is a special kind of tree in which the parent node can have at most 2 children. An Example Binary Tree is shown below.
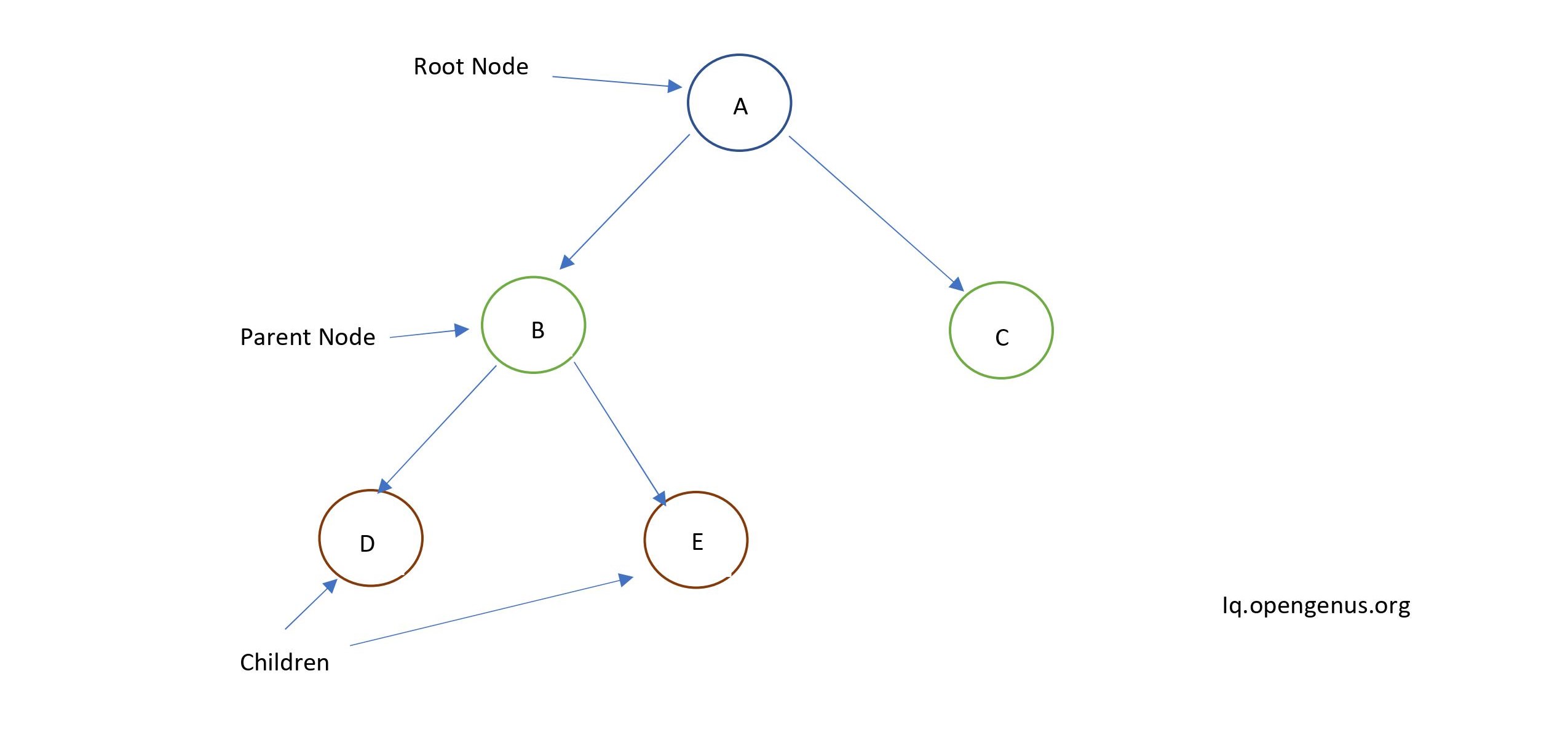
Introduction to Time and Space Complexity
Time Complexity is defined as the time taken by an algorithm to run to its completion. It's a measure of how efficient an algorithm is. We Ideally want a algorithm with lower time complexity.
Space complexity is defined as the total space required for a program to complete its execution.
Operations on Binary Tree
Binary Tree supports various operations such as Insertion , Deletion , Traversals , Searching. We shall be discussing each operations with its Space and Time complexity.
Insert operation in Binary Tree
Insertion refers to the act of adding another node to the existing binary tree .
Consider the Tree as :
a Level 0
/ \
b c Level 1
/
d Level 2
Insertion would happen at the lowest level , where we have space to add further nodes. In this case , at level 2 we can add another node. After the Addition of another node , the Tree would look like:
a Level 0
/ \
b c Level 1
/ \
d e Level 2
Worst Case Time Complexity of Insertion
-
Worst Case Scenario : The Worst case scenario would occur when we the tree is totally skewed in one direction , i.e Left or Right , an Example is given below
a / b / c / d
In the worst case , the height of the tree would be equal to the number of nodes in the tree , which is N. Therefore all the nodes must be traversed to add a new node.
thus , time complexity would be O(N).
Best Case Time Complexity of Insertion
- Best Case Scenario : In the best case scenario , the tree would be divided into 2 sub trees which are perfectly balanced.Balanced binary tree also known as height balanced tree is defined as a binary tree in which the difference between the height of the left subtree and right subtree is not more than m, where m is usually equal to 1.
Consider the example below :
a
/ \
b c
/ \ /
d e f
In the above binary tree , we can see the height difference between the left subtree and right subtree is 0 , which is less than 1.If we were to add a value into the tree , the resultant tree would look like:
a
/ \
b c
/ \ / \
d e f g
We know that when we have N nodes which are evenly distributed in a binary tree , then the height of the tree is defined as Log N , which is the number of nodes we need to travel for the insertion , thus the runtime for insertion is O(Log N).
Average Case Time Complexity of Insertion
- Average Case Scenario: Average height of a binary tree is O(N0.5) ,
You may read more about it in the references section. Insertion depends on the height of the binary tree , thus the runtime is O(N0.5)
Searching / Find Operation
Searching refers to the act of finding whether a value is present in the binary tree or not.
a
/ \
b c
In the above example , if we search for a value say a ,we would find it. if we search for a value which is not present in the tree , usually Null is returned in that case.
Worst Case Time Complexity of Search
-
Worst Case Scenario: In Worst case scenario , we consider a skewed tree , either left or right skewed. Consider an example where we have to find the last node (in our example it being d), then in that case we have to travel all the nodes of the tree , which is the height of the tree. As the height is N in worst case , runtime is also be O(N)
a / b / c / d
Best Case Time Complexity of Search
- Best Case Scenario : In Best case scenario , We assume that the root element is the one that is being searching , as it is the first element the time complexity is constant O(1)
Average Case Time Complexity of Search
- Average Case Scenario: Just Like Insertion , Average Case is dependent on the average height of the binary tree , which is N0.5 , thus average runtime is O(N0.5)
Deletion Operation
Deletion refers to the act of removal of a node from the binary tree , in deletion we remove the element by replacing it with the rightmost element and delete the rightmost leaf node when it is replaced. We don't consider the order of elements in a normal binary tree.
a
/ \
b c
/ \ /
d e f
Consider that we need to delete b from the tree , then what we do is replace b with f and then delete b from the tree. The resultant figure would look like:
a
/ \
f c
/ \
d e
Worst Case Time Complexity of Delete
-
Worst Case Scenario: In Worst Case Scenario , we assume that we are going to delete leftmost node of a tree which is having 2 skewed trees of opposite direction as it's subtrees , then All the nodes of the tree have to be visited for the tree to complete the deletion , thus runtime of worst case is O(N)
a / \ b c / \ d f
here , if we wanted to delete d from the tree , then first we have to find if d is present in the tree , if it is then find the rightmost leaf node and exchange them and delete the rightmost node.
Average Case Time Complexity of Delete
- Average Case Scenario: Just Like Insertion and Searching , Average Case is dependent on the average height of the binary tree , which is N0.5 , thus average runtime is O(N0.5)
Best Case Time Complexity of Delete
- Best Case Scenario : In Deletion , if we had to delete the rightmost leaf node , then the cost of deletion is O(logN) as we need to traverse to the leaf node and the least cost of traversing to leaf node is O(logN).
Space Complexity of Insert, Search and Delete
With Insertion , Deletion and Searching having a Average tree height of N0.5 , there would be that many calls on the stack during execution , thus the average Space complexity would be (N0.5) if the operations are implemented recursively.
If the operations are implemented iteratively, the space complexity of all three operations (insert, search, delete) will be O(1).
Conclusion
Time Complexity of different operations in Binary Tree:
| Operation | Worst Case | Average Case | Best Case |
|---|---|---|---|
| Insert | O(N) | O(N0.5) | O(logN) |
| Search | O(N) | O(N0.5) | O(1) |
| Delete | O(N) | O(N0.5) | O(logN) |
Space Complexity of different operations in Binary Tree:
| Operation | Iterative) | Recursive, average |
| Insert | O(1) | O(H) = O(N0.5) |
| Search | O(1) | O(H) = O(N0.5) |
| Delete | O(1) | O(H) = O(N0.5) |
where N = number of nodes in Binary Tree, H = height of Binary Tree
A Binary Tree is a very useful data structure used to store data in a hierarchical manner , but there are certain issues like the average time for each operation be it insertion , deletion or searching taking (N0.5) , which is still higher than average of Log N promised by Binary Search Trees , thus they are preferred over simple binary trees.
With this article at OpenGenus, you must have the complete idea of Time & Space Complexity of Binary Tree operations.
