Trie in C Programming Language (using struct)

Overview of Trie

Prefix trees, sometimes referred to as Trie data structures, are tree-like data structures used for effective string storing and retrieval. The use of intensive string operations in activities like IP routing, auto completion, spell checking, and looking up words or prefixes in dictionaries is where it shines.

The Trie categorizes data by decomposing each string into its component characters and arranging them in a hierarchical order. Every node in the trie represents a character, and the edges extending from the nodes reflect the potential characters that may come after that character. It is possible to effectively search, insert, or remove strings by moving through the Trie.

Representation of Trie

The trie representation of a string is a compact way to store a set of strings. It is also a efficient way to search for strings in the set, as the search can be done by traversing the trie from the root node to the leaf node that represents the string.

To represent a Trie data structure in C, you can use a structure and pointers to create the nodes of the Trie.

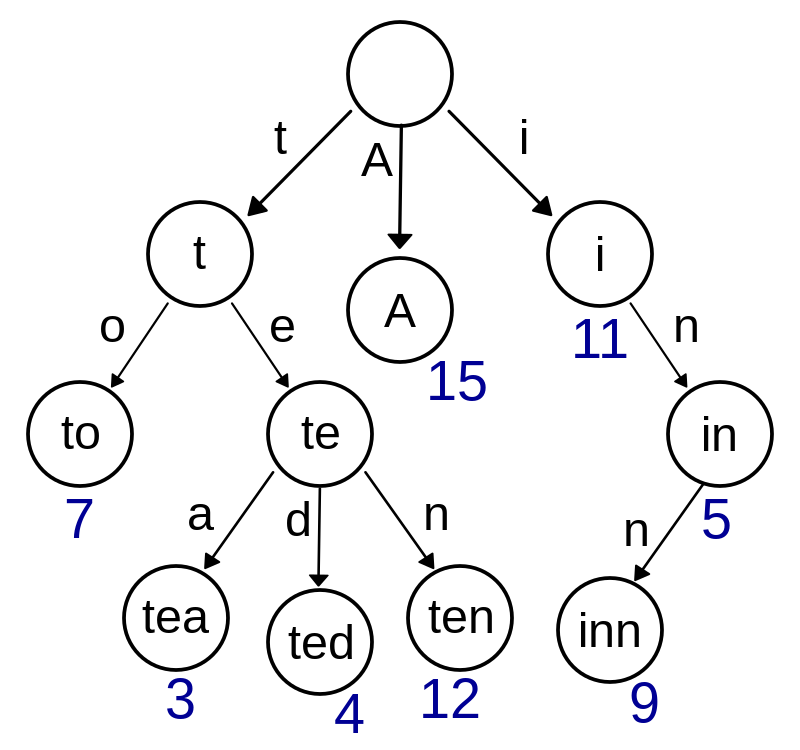
As in this case for example the empty node is the root from which all other strings emerge as in this case from root node the next node is t ,A and i followed by 't' is 'o' to give us the string 'to'. And in the same way we get tea, ted, ten and inn.
Data Structure of Trie:

1. Trie Node: Each node in the Trie represents a character. It contains the following components:

• Character Representation: The character associated with the node.
• Children Pointers: Pointers to child nodes, typically stored in an array or a hash map. The number of children corresponds to the size of the alphabet or the possible characters that can follow the current node.
• End of Word Marker: A flag that indicates whether the node represents the end of a word or not.

2.Root Node: The topmost node in the Trie. It serves as the entry point for accessing the Trie and does not correspond to any character.

3.Child Nodes: The nodes that follow a parent node in the Trie hierarchy. Each child node represents the next character in a word or string.

4.Leaf Nodes: The nodes that mark the end of a word. They typically have the end of word marker set to indicate that a complete word has been stored.

5.Path and Prefix: The path from the root to a particular node represents a sequence of characters. A prefix is a sequence of characters that forms the beginning of a word stored in the Trie.

Implementation of Trie

Implementation in Trie mainly involves 3 operations:

1. Insertion.
2. Searching
3. Deletion

In this code, the main function demonstrates the usage of the Trie data structure. It creates a root node, inserts words into the Trie using the insert function, searches for words using the search function, deletes a word using the delete function.

#include <stdio.h>
#include <stdlib.h>

typedef struct TrieNode {
  struct TrieNode* children[26];
  int is_end;
} TrieNode;

• typedef struct TrieNode: This line introduces a new data type, TrieNode, which represents a node in the Trie.
• struct TrieNode* children[26];: There is an array named children within the TrieNode struct that stores references to additional TrieNode structs. The array has a capacity of 26, which means it may store references to 26 child nodes. This relates to the English alphabet's 26 letters.
• int is_end; specifies whether the current node marks the end of a word. If is_end is set to 1 (true), the node represents the end of a word in the Trie. If the value is 0 (false), the node does not reflect the end of any word.

TrieNode* createTrieNode() {
  TrieNode* node = (TrieNode*)malloc(sizeof(TrieNode));
  for (int i = 0; i < 26; i++) {
    node->children[i] = NULL;
  }
  node->is_end = 0;
  return node;
}

• The createTrieNode() method allocates memory for a new Trie node, sets its children to NULL, sets the is_end flag to 0, and returns the node pointer.

void insertTrie(TrieNode* root, char* word) {
  TrieNode* current_node = root;
  for (int i = 0; word[i] != '\0'; i++) {
    int index = word[i] - 'a';
    if (current_node->children[index] == NULL) {
      current_node->children[index] = createTrieNode();
    }
    current_node = current_node->children[index];
  }
  current_node->is_end = 1;
}

• insertTrie(): This function adds a new word to the Trie. It begins at the root node and proceeds through the word's characters one by one. If the current character's child pointer is NULL, it generates a new TrieNode and sets the child pointer to it. It then continues on to the following character in the word. When it reaches the end of the word, it changes the current node's is_end flag to 1.

int searchTrie(TrieNode* root, char* word) {
  TrieNode* current_node = root;
  for (int i = 0; word[i] != '\0'; i++) {
    int index = word[i] - 'a';
    if (current_node->children[index] == NULL) {
      return 0;
    }
    current_node = current_node->children[index];
  }
  return current_node->is_end;
}

• searchTrie(): This function searches the Trie for a word. It begins at the root node and proceeds through the word's characters one by one. If the current character's child pointer is NULL, the method returns 0. Otherwise, it advances to the following character in the word. When it reaches the end of the word, it returns 1 if the current node's is_end flag is set to 1, and 0 otherwise.

void deleteTrie(TrieNode* root, char* word) {
  if (root == NULL) {
    return;
  }

  if (word[0] == '\0') {
    root->is_end = 0;
    return;
  }

  int index = word[0] - 'a';
  deleteTrie(root->children[index], word + 1);

  if (root->children[index] == NULL && !root->is_end) {
    free(root);
    root = NULL;
  }
}

• deleteTrie(): The delete function removes a word from the Trie. It begins at the root node and proceeds through the word's characters one by one. The method returns if the child pointer at the current character is NULL. Otherwise, it recursively calls itself on the child node. When it reaches the end of the word, it changes the current node's is_end flag to 0. The function frees the current node if it has no children and its is_end flag is not set.

int main() {
  TrieNode* root = createTrieNode();
  insertTrie(root, "hello");
  insertTrie(root, "world");
  printf("Is 'hello' present? \n") ;
  int x = searchTrie(root, "hello");
  if(x==1)printf("Yes\n");
   else printf("No\n");
  printf("Is 'world' present? \n");
  int y = searchTrie(root, "world");
  if(y==1)printf("Yes\n");
   else printf("No\n");
  deleteTrie(root, "hello");
  printf("Is 'hello' present? \n");
  int z = searchTrie(root, "hello");
  if(z==1)printf("Yes\n");
   else printf("No\n");
  return 0;
}

This main() function constructs a Trie, inserts the words "hello" and "world," tests their presence in the Trie, deletes the word "hello," and then checks its presence again after deletion. The programme prints the existence of each word in the Trie at different levels.

OUTPUT:

Is 'hello' present? 
Yes
Is 'world' present? 
Yes
Is 'hello' present? 
No

Conclusion:

In conclusion,the Trie data structure, also known as a prefix tree, is a quick and easy way to store and retrieve strings. It organises strings hierarchically, allowing for quick searches, insertions, and removals. Tries are extensively employed in a variety of applications, including IP routing, auto-completion, spell-checking, and dictionary word lookup.

To summarize this article at OpenGenus, understanding the Trie data structure and its implementation might be beneficial in tackling many string-related issues quickly. It is a versatile and powerful tool that may considerably increase the performance of algorithms and applications that operate with strings.