Iterative In-order Traversal

In this article, we have explored the concept of Iterative In-order Traversal along with detailed step by step example and complete implementation.

Table of contents

1. Definitions
2. Algorithm
3. Time complexity
4. A way of implementation

1. Definitions

Binary trees are data structures where each node contains only 2 references to other nodes. Usually they are called left and right, but you can name it in other ways too, for ex: up and down or yin and yang, and so on.

There are different ways to traverse a tree. One of them is inorder, meaning a node is visiting:
* firstly the left node of it
* secondly its value
* thirdly the right node of it

We can do that recursively or iteratively.
For comparasion we will aproach the both ways.

2. Algorithm

Iterative pseudocode algorithm of inorder traversal of a binary tree is as follow 1 :

procedure visitNode(node)
    stack ← empty stack
    while not stack is not empty or node is not null
        if node is not null
            stack.push(node)
            node ← node.left
        else
            node ← stack.pop()
            visit(node)
            node ← node.right

Notice the use of a stack that means a LIFO data structure that keeps the values of the visitted nodes.

3. Time complexity

For a Graph, the complexity of a Depth First Traversal is O(n + m), where n is the number of nodes, and m is the number of edges.

Since a Binary Tree is also a Graph, the same applies here. The complexity of each of these Depth-first traversals is O(n+m).

Since the number of edges that can originate from a node is limited to 2 in the case of a Binary Tree, the maximum number of total edges in a Binary Tree is n-1, where n is the total number of nodes.

The complexity then becomes O(n + n-1), which is O(n).

4. A way of implementation

The next program will use the recursive and iterative functions to traverse the binary tree and the stack library to keep the node values. If we would like not to use that library then we would have need to implement one by ourselves.

#include <iostream>
#include <stack>

using namespace std;

struct Node
{
    int val;
    Node *left = NULL;
    Node *right = NULL;
};

void visitNodeRecursive(Node *n)
{
    if (n != NULL)
        {
            visitNodeRecursive(n->left);
            cout << n->val<<" ";
            visitNodeRecursive(n->right);
        }
}

void visitNodeIterative(Node *n)
{
    stack<Node *> s;
    
    while ( ! s.empty() || n != NULL)
        {
            if (n != NULL)
                {
                    s.push(n);
                    n = n->left;
                }
            else
                {   n = s.top();
                    cout<< n->val<<" ";
                    s.pop();
                    n = n->right;
                }
        }
}

int main()
{
    Node n1,n2,n3,n4,n5,n6,n7;
    n1.val = 1;
    n2.val = 2;
    n3.val = 3;
    n4.val = 4;
    n5.val = 5;
    n6.val = 6;
    n7.val = 7;
    
    n1.left = &n2;
    n1.right = &n3;
    
    n2.left = &n4;
    n2.right = &n6;
    
    n3.left = &n5;
    //n3.right = NULL;
    
    //n4.left = NULL;
    n4.right = &n7;
    
    //n5.left = NULL;
    //n5.right = NULL;
    
    //n6.left = NULL;
    //n6.right = NULL;
    
    //n7.left = NULL;
    //n7.right = NULL;
    
    visitNodeRecursive(&n1);
    cout<<endl;
    visitNodeIterative(&n1);
    
    return 0;
}

Output:

4 7 2 6 1 5 3
4 7 2 6 1 5 3

In this implementation we have declared 7 objects of type Node.
A Node is of a struct type. You can also use the class type implementation.

The structure of the above binary tree will look like this:

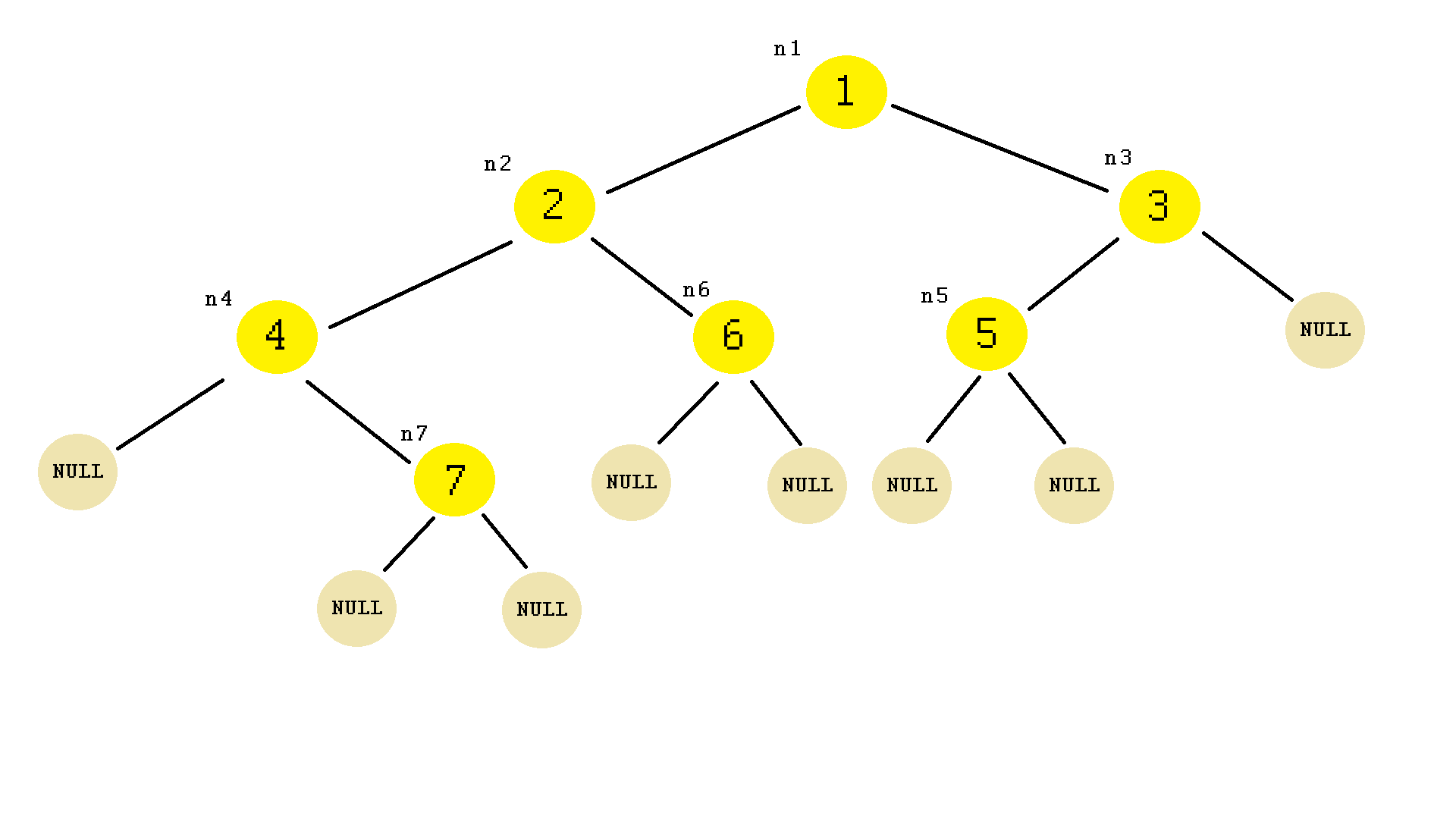
Notice the initialization with NULL of the left and right Node pointers which is a key point in the implementation of the binary tree structure. If we would not use that then we would have needed to initialize all the empty references with NULL when declaring the objects and that is because of the checking condition where a node needs to be different than NULL, similar to what it has been written in the comments. Try not to do that and you'll have another result.

Case by case example of the iterative traversal using the stack: