
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have solved the Two Sum Problem in Binary Search Tree using three different approaches involving Depth First Search, Inorder Traversal and Augmented Binary Search Tree.
Table of content:
- Problem Statement
- Approach 1: Using DFS
- Approach 2: Using Inorder traversal
- Approach 3: Using Augmented BST
Let us get started.
Problem Statement
Given a Binary Search Tree and an integer k, we have to determine if there exist two nodes in the the BST with sum of values equal to the given target. The input is root of the tree and output can be true or false.
For example,
The given Binary Search Tree is:
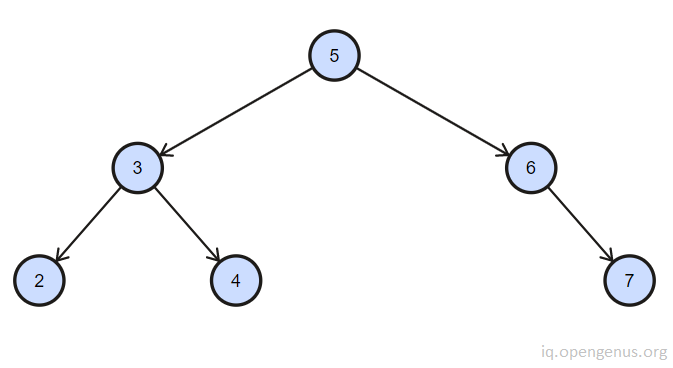
Input: root = [5, 3, 6, 2, 4, null, 7], k = 9
Output: true
Explanation: Nodes (3,6), (5,4) and (2,7) have sum equal to 9.
This problem can be solved using the approaches as discussed below.
Approach 1: Using DFS
In this approach, we will do a DFS (depth first search) traversal of the tree and look for pairs with the given target. This can be performed efficiently using hashtable.(O(1) time for lookup).
We can create a hashtable using hashset in java or unordered_set in C++ to store the values of the nodes that we encountered. If the current node and any of the stored values sum up to target, then we found a pair and return true. If we reach the end of the tree, we return false.
Steps of this approach:
- Let sum be S and define a Hashtable H
- Do a DFS traversal of Binary Search Tree B
2.1. For every node N, check if S-N exists in hashtable H
2.2. If S-N exists, then return TRUE
2.3. If S-N does not exist, insert N in hashtable H - If no pair is found, return FALSE.
C++ Code:
/*
// Structure of the Tree node.
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
}
*/
bool findPair(TreeNode * root, int k){
unordered_set<int> values; // to store the values
return dfs(root, k, values);
}
bool dfs(TreeNode* root, int k, unordered_set<int> &values){
// If complement not found beyond the leaf node, then return false;
if(root == NULL) return false;
// Find the complement of the current node in the hash table.
// If found complement, then return true.
if(values.find(k - root -> val) != values.end()){
return true;
}
//Insert the current node value in hashtable.
values.insert(root -> val);
// Same process for node in left and right subtrees.
return dfs(root -> left, k, values) ||
dfs(root -> right, k, values);
}
Time complexity : O(N)
Space complexity: O(N)
Where n is the number of nodes in BST.
This approach can be applied on any tree. We can particularly use the special property of BST to solve the problem.
Approach 2: Using Inorder traversal
In this approach, we can store the node values of the tree in an array using inorder traversal. As we know that the inorder traversal of BST is sorted, we can use two pointers to find the desired pair. We can use two pointers on start and end of the array and search for the target.
Steps of this approach:
- Let the sum be S.
- Traverse Binary Search Tree B and store inorder traverse I.
- Use 2 pointer technique (one pointer at start and other pointer at end) to find a pair where the sum is equal to S.
C++ Code:
// Function to store the inorder traversal in array.
void inorder(vector<int> &nodes, TreeNode *root){
if(root == NULL)return;
inorder(nodes, root -> left);
nodes.push_back(root -> val);
inorder(nodes, root -> right);
}
// Function to search pair in array using two pointers.
bool twoPointers(vector<int> &nodes, int k){
// left and right pointer
int l = 0, r = nodes.size() - 1;
while(l < r){
int sum = nodes[l] + nodes[r];
if(sum == k)return true; //If found valid pair, return true.
else if(sum < k) l++;
else if(sum > k) r--;
}
return false; // If pair not found, return false.
}
// Given Function
bool findPair(TreeNode* root, int k) {
vector<int> nodes;
inorder(nodes, root);
return twoPointers(nodes, k);
}
Time Complexity: O(n)
Space Complexity: O(n)
Where n is number of nodes in BST.
Approach 3: Using Augmented BST
This approach can be used to optimize the space complexity of the problem. The intuition is, we can keep a left and right pointer to the leftmost leaf node and rightmost leaf node in the BST. We can find the sum of the node values pointed by the two pointers.
As the structure of Binary Search Tree is modified, this technique is known as Augmented BST.
If the sum is greater than target, then we can move the right pointer to previous greater node, or predecessor.
If the sum is less than the target, we can move the left pointer to next greater node or successor.
This approach works in O(1) space and O(nlogn) time because we will traverse all the nodes in worst case and the findNext() and findPrevious() functions take O(logn) time in worst case.
Implementation in C++:
bool findPairs(TreeNode* root, int k){
if (root == NULL) {
return false;
}
TreeNode* start = root;
TreeNode* end = root;
// start pointer will point to leftmost leaf.
while (start -> left != NULL) {
start = start -> left;
}
//end pointer will point to rightmost leaf.
while (end -> right != NULL) {
end = end -> right;
}
// check for sum of nodes pointed by two pointers,
//if equal to target then return true.
while (start != end) {
int sum = start -> val + end -> val;
// end pointer is moved to previous greater node.
if (sum > k) {
end = findPrevious(root, end);
}
// start pointer is moved to next greater node.
else if (sum < k) {
start = findNext(root, start);
}
else {
return true;
}
}
return false; // if pair not found, return false.
}
TreeNode* findPrevious(TreeNode* root, TreeNode* end) {
TreeNode* pred = NULL; // pointer to the desired node.
TreeNode* now = root; // pointer to traverse tree.
while (now != NULL) {
if (now -> val < end -> val) {
pred = now;
now = now -> right;
} else {
now = now -> left;
}
}
return pred;
}
TreeNode* findNext(TreeNode* root, TreeNode* start) {
TreeNode* succ = NULL; // pointer to the desired node.
TreeNode* now = root; // pointer to traverse tree.
while (now != NULL) {
if (now -> val > start -> val) {
succ = now;
now = now -> left;
} else {
now = now -> right;
}
}
return succ;
}
Time complexity: O(N logN)
Space complexity: O(1)
Where n is the number of nodes.
These methods can be used to find the pair with given sum in the BST.
With this article at OpenGenus, you must have a complete idea of solving this problem of two sum in BST in multiple ways.
