Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
A Binary Search Tree (BST) is usually implemented using NULLs in C or C++. This article explores an alternative approach of using placeholder nodes. Here the Binary Search Tree will be implemented in C++.
Introduction
Introduction to BST
A binary tree is a tree where each node can have at most two child nodes: the left child node and the right child node. A Binary Search Tree (BST) is a binary tree with an additional property that for each node N, its left child node has a key less than the value of node N and the right child node has a key greater than the value of node N. Here we have assumed all keys to be unique.
The usual implementation
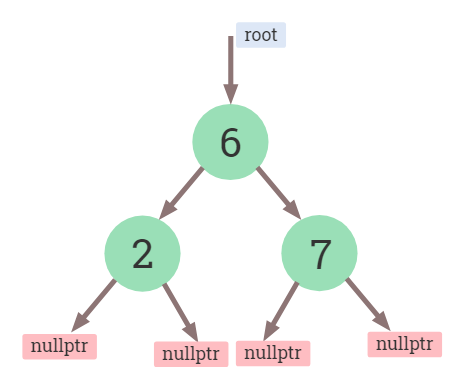
In the implementation of Binary Search Tree, each node contains a left pointer, a right pointer, and a key element. The root pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller subtrees on either side. A null pointer represents a binary tree with no elements (i.e., the empty tree).
For the purpose of this article, we'll assume that the node stores an integer and two pointers for the left and right child nodes.
Use of NULL
NULL is the null pointer literal used in C and sometimes even in C++. It defines a null pointer value. In the BST, they are used to indicate the absence of a node.
The NULL values are a useful implementation feature but in reality, it is advised to avoid using NULL in designing software as it increases the number of edge cases and needs to be handled separately. The prominent reason for this is due to the fact that NULL represents both the value 0 and a null pointer literal. Thus it's usage is not type safe.
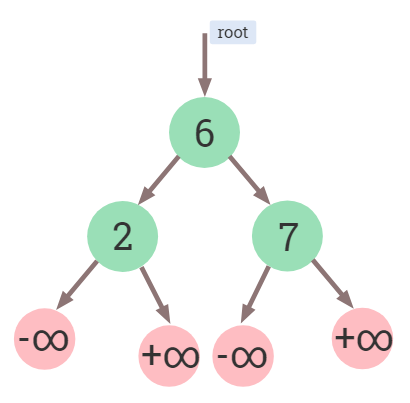
Placeholder nodes
In our implementation, the placeholder nodes (instead of NULL) indicate the absence of a node. Since we'll be using nodes themselves to indicate absence of nodes, we need a way to differentiate them. We could ideally assume that their key values are negative infinity or positive infinity. But we can't really use infinity, so we use use the value of macros INT_MIN and INT_MAX defined in header <climits> for the left and right nodes respectively.
The reason of using INT_MIN and INT_MAX values is because we assume that they are small enough and large enough respectively to not be used in other nodes.
Checking for placeholder nodes
We need a way to determine if a node is a placeholder node. So we define a function isPlaceholderNode() to do that. This is analogous to checking for NULL value in the usual implementation.
// a placeholder node is characterized by its key value
// returns true/false depending on whether or
// not the node is a placeholder node
bool isPlaceholderNode(node* n)
{
return n->key == INT_MAX || n->key == INT_MIN;
}
BST nodes
The node contains an integer key and two pointers left and right. This is similar to struct used in conventional binary search tree, but we'll use some features of C++.
struct node{
int key;
node* left;
node* right;
node(int key): key(key), left(nullptr), right(nullptr) {}
};
Due to this there's a constructor and member initialization is done in the initializer list.
Creating a BST node
We'll use a function that returns a pointer to a newly created node. The node would have two placeholder nodes (in place of NULL)
node* getNewNode(int key){
node* t;
t = new node(key); // node
t->left = new node(INT_MIN); // placeholder node
t->right = new node(INT_MAX); // placeholder node
return t;
}
BST operations
Inserting a node
A new node is always inserted as a leaf node. If the tree is empty we insert the node as root. If the tree is non-empty then to insert a node we start from the root node and if the node to insert is less than the root, we go to left child, otherwise we go to the right child of the root. We continue this traversal until we find a placeholder node (or a leaf node) where we cannot go any further. We then insert the node as a left or right child of the leaf node depending on whether the node is less or greater than the leaf node.
Note that we have to replace the placeholder node for insertion. i.e., delete the placeholder node first and then insert a new node.
node* insertNode(node* root, int key)
{
// insert the node by first 'deleting' the placeholder node
if (isPlaceholderNode(root)){
delete(root);
return getNewNode(key);
}
// to determine a place to insert the node, traverse left
if (key < root->key){
root->left = insertNode(root->left, key);
}
else{ // or traverse right
root->right = insertNode(root->right, key);
}
return root;
}
Deleting a node
Deleting a node has several cases, depending on the type of node we want to delete. For convenience lets assume the node to be deleted is N
Nis a leaf node (i.e., has no child nodes) - In this case we just delete the node.- node to delete has one child node - In this case we cannot directly delete the node. So we first promote its child node to its place here if the node to be deleted is a left child of the parent, then we connect the left pointer of the parent (of the deleted node) to the single child. Otherwise if the node to be deleted is a right child of the parent, then we connect the right pointer of the parent (of the deleted node) to single child.
- node to delete has two child nodes - In this case the node
Nto be deleted has two sub-trees. here we need to find the minimum node in the right sub-tree of nodeNand then replace it withN. In the code we useminValueNode(root->right)to find the minimum value in the right sub-tree.
node* deleteNode(node* root, int key)
{
// node not found
if(isPlaceholderNode(root)){
return root;
}
if(key < (root->key)){ // traverse left
root->left = deleteNode((root->left), key);
}
else if (key > (root->key)){ // traverse right
root->right = deleteNode((root->right), key);
}
else{ // node found
// case: node has zero / one right child node
if (isPlaceholderNode(root->left)){
node *temp = root->right;
delete(root);
return temp;
}
// case: node has one left-child node
else if (isPlaceholderNode(root->right)){
node *temp = root->left;
delete(root);
return temp;
}
// case: node with both children
// get successor and then delete the node
node* temp = minValueNode(root->right);
// Copy the inorder successor's content to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
The minValueNode() function is implemented as below
node* minValueNode(node* root)
{
node* current = root;
// search the leftmost tree
while (!isPlaceholderNode(current)
&& !isPlaceholderNode(current->left)){
current = current->left;
}
return current;
}
Searching for a key
Suppose we are searching for a key K. When we are at some node. If this node has the key that we're searching for, then the search is over and we return true. Otherwise, the key at the current node is either smaller or greater than K.
By using the BST property, we know for any root, its left sub-tree will have key values less than that of root, and its right sub-tree will have key values greater than that of root, thus we decide to traverse left or right.
bool search(node* root, int key){
if(!isPlaceholderNode(root)){
if(root->key == key){ // found
return true;
}
else{
if(root->key > key){
// check in left sub-tree
return search(root->left, key);
}
else{
// check in right sub-tree
return search(root->right, key);
}
}
}
else{
// empty sub-tree
return false;
}
}
Inorder traversal
To print the tree, we use the inorder traversal in this implementation. Inorder traversal always produces the keys in a sorted order. The reason for this is due to the order of visits. For any root, the left sub-tree of the root is visited first then the root is visited and then finally the right sub-tree is visited.
In the function given below we first check if the pointer root is pointing to a placeholder node. If it is then, it means that the sub-tree is empty, in which case it returns, else it recursively traverses the left sub-tree and then prints the root and then recursively traverses the right subtree.
void inorder(node *root)
{
if (!isPlaceholderNode(root)){
// print left first, then root and then right
inorder(root->left);
cout << (root->key) << " ";
inorder(root->right);
}
}
Conclusion
While the important functions were covered for the placeholder nodes based BST. The complete implementation is in [this code].(https://github.com/RohitTopi/opengenus/blob/main/BST_no_null.cpp).