Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
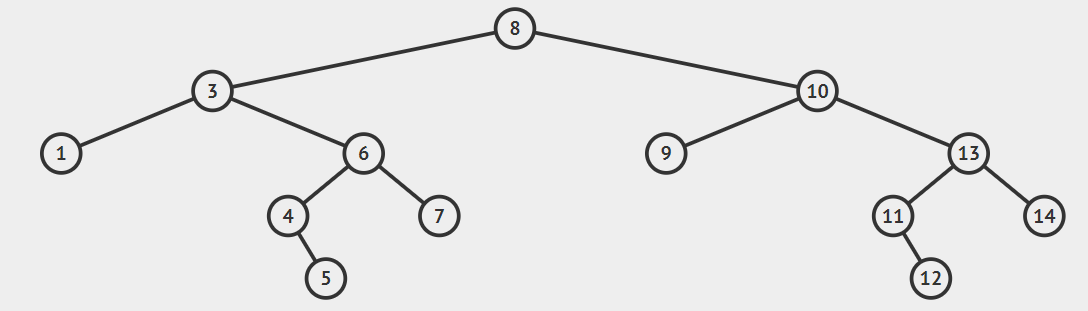
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
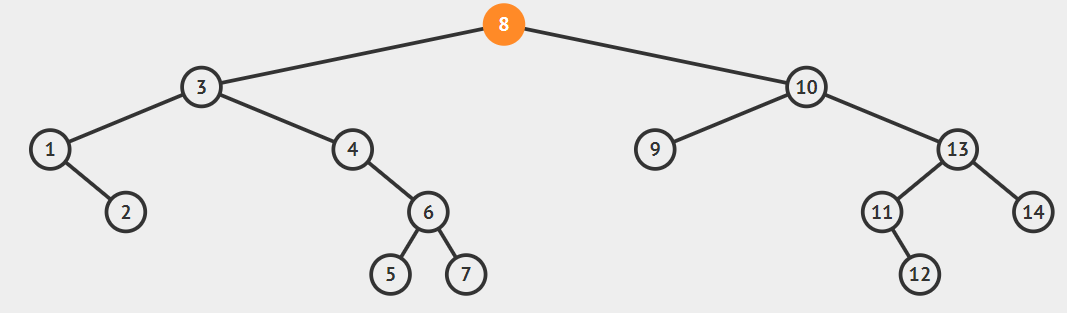
Below is the Example of Binary Search Tree.
Background: The worst case time complexity of search and insert operations is O(h) where h is height of Binary Search Tree. In worst case, we may have to travel from root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of search and insert operation may become O(n).
Algorithm for finding minimum or maximum element in Binary Search Tree
As we know the Property of Binary search tree.This quite simple
Approch for finding minimum element:
- Traverse the node from root to left recursively until left is NULL.
- The node whose left is NULL is the node with minimum value.
Approch for finding maximum element:
- Traverse the node from root to right recursively until right is NULL.
- The node whose right is NULL is the node with maximum value.
Implementation of the above approches.
// C++ program to find maximum or minimum element in binary search tree
#include <bits/stdc++.h>
using namespace std;
struct node
{
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
struct node *newNode(int );
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree,
return the minimum data value found in that
tree. Note that the entire tree does not need
to be searched. */
int minValue(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
{
current = current->left;
}
return(current->key);
}
/* Given a non-empty binary search tree,
return the maximum data value found in that
tree. Note that the entire tree does not need
to be searched. */
int maxValue(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while (current->right != NULL)
{
current = current->right;
}
return(current->key);
}
// Driver Program to test above functions
int main()
{
int maxValue(struct node* );
struct node* insert(struct node* , int );
int minValue(struct node* );
struct node *root = NULL;
root = insert(root, 8);
insert(root, 3);
insert(root, 10);
insert(root, 1);
insert(root, 6);
insert(root, 4);
insert(root, 7);
insert(root, 5);
insert(root, 10);
insert(root, 9);
insert(root, 13);
insert(root, 11);
insert(root, 14);
insert(root, 12);
insert(root, 2);
cout << "\n Minimum value in BST is " << minValue(root)<<endl;
cout << "\n Maximum value in BST is " << maxValue(root);
return 0;
}
Output:
Minimum value in BST is 1
Maximum value in BST is 14
Explanation:
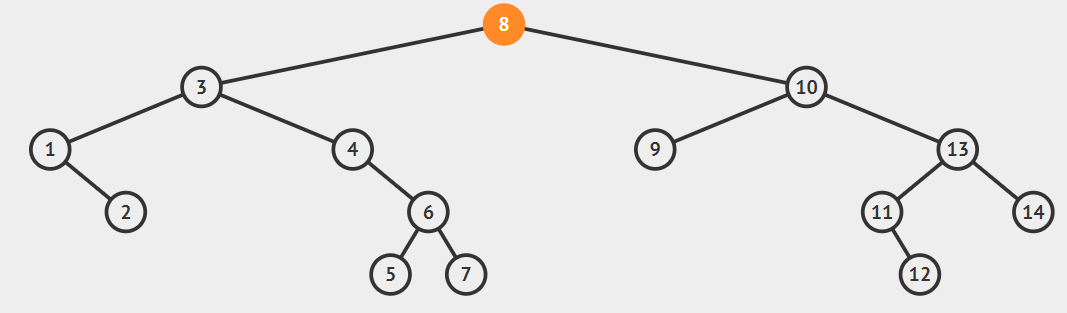
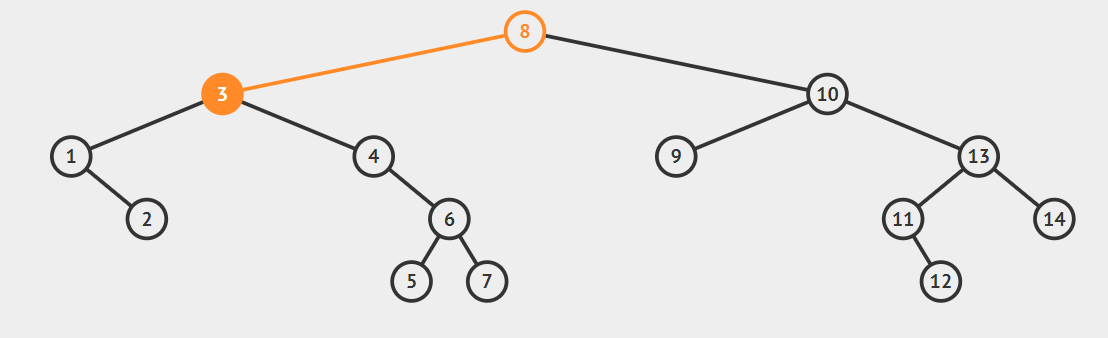
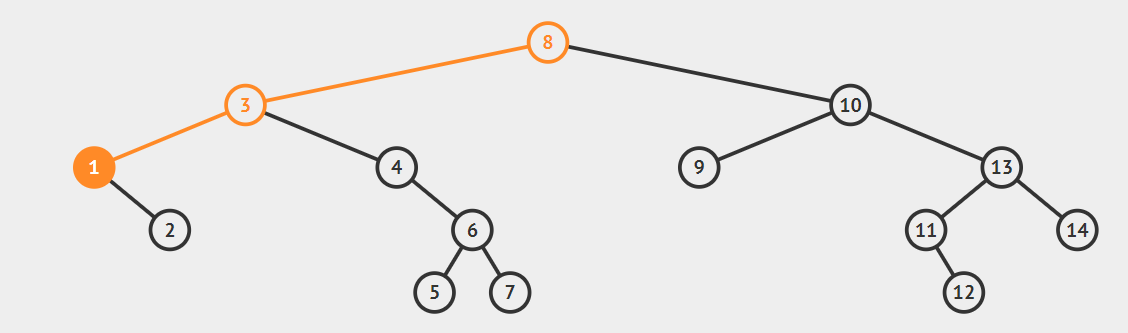
For Finding Minimum value in Binary search tree.
- start from root i.e 8.
- As left of root is not null go to left of root i.e 3.
- As left of 3 is not null go to left of 3 i.e. 1.
- Now as the left of 1 is null therefore 1 is the minimum element
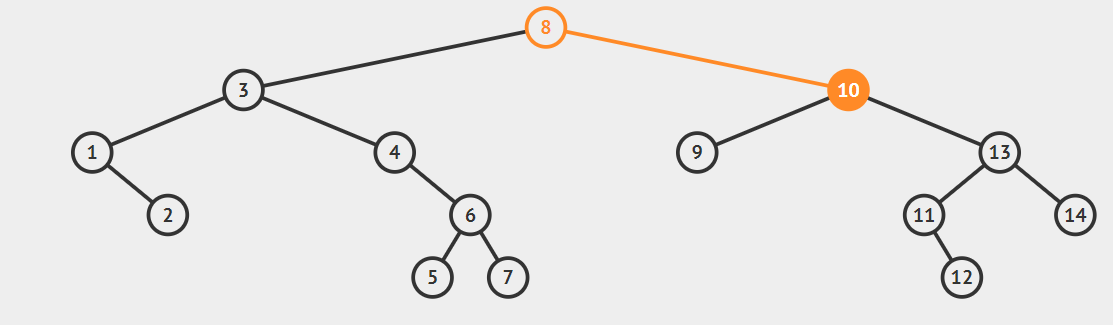
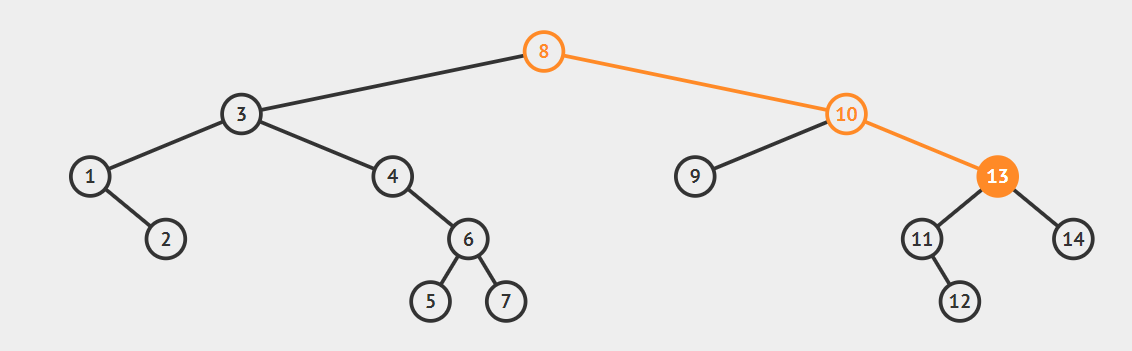
For Finding Maximum value in Binary search tree. - start from root i.e 8.
- As right of root is not null go to right of root i.e 10.
- As right of 10 is not null go to right of root i.e 13.
- As right of 13 is not null go to right of root i.e 14.
- Now as the right of 14 is null therefore 14 is the maximum element.
Time Complexity:
O(N) Worst case happens for left skewed trees in finding the minimum value.
O(N) Worst case happens for right skewed trees in finding the maximum value.
O(1) Best case happens for left skewed trees in finding the maximum value.
O(1) Best case happens for right skewed trees in finding the minimum value.
In the balanced Binary Search tree, the time complexity is O(log N)
N is the number of elements in a Binary Search tree