Table of content

1. Basics of BST
2. Deep understanding of AVL trees
3. AVL Tree Operations & Implementations
   • Insertion
   • Deletion
   • Different rotations
   • Searching
   • Minimum and Maximum
4. Final Implementation
5. Time and Space Complexity
6. Questions

Basics of BST

A Binary Search Tree (BST) is a type of binary tree data structure in which nodes are connected by edges. Each node has at most two children, commonly referred to as the left child and the right child.

It maintains a specific order among its nodes. For each node in the tree, all nodes in its left subtree have keys less than the node's key, and all nodes in its right subtree have keys greater than the node's key.
This property makes BSTs efficient for searching, insertion, and deletion operations, as it allows for faster traversal and retrieval of elements. The BST's ordered structure enables various applications, including efficient sorting algorithms and quick lookup of data with a specific key.

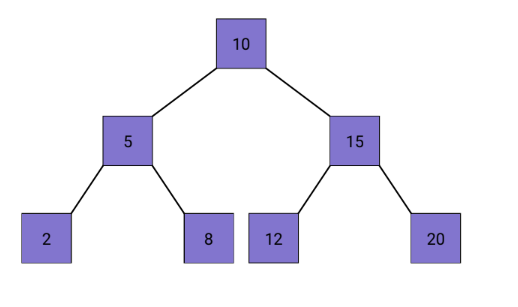
Complexity Analysis of BST:

A balanced BST has logarithmic height (O(log n)) for average operations (insertion, deletion, search), but can degrade to O(n) in the worst case.

To maintain efficiency by ensuring logarithmic height even in worst-case scenarios, balanced variants like AVL trees and Red-Black trees are used.

Deep Understanding of AVL Trees

AVL (Adelson-Velsky and Landis) tree is a self-balancing binary search tree, where the balance factor of each node is the difference between the heights of its left and right subtrees i.e. either -1, 0, or 1.

In a regular binary search tree, sometimes one side can become much taller than the other, making it non-uniform. This can slow down operations like searching for values.

To avoid this problem, an AVL tree constantly checks the heights of its left and right subtrees. It makes sure that the difference between these heights is never more than 1 (either -1, 0, or 1). If it gets out of balance, the AVL tree performs rotations to bring it back into balance.

By doing this, the AVL tree remains approximately balanced all the time. This means that operations like searching, inserting, and deleting values are much faster compared to regular binary search trees, even when dealing with a large number of elements.

Core Aspects of AVL Trees:

• Balance Factor: For every node in an AVL tree, the balance factor is calculated as follows:
  [Balance Factor = Height of Left Subtree - Height of Right Subtree]

• Balance Condition: The balance factor of each node in an AVL tree must be one of {-1, 0, 1}. If the balance factor of any node violates this condition (i.e., becomes greater than 1 or less than -1), the tree is unbalanced.

• Height Property: The height of an AVL tree is defined as the length of the longest path from the root node to a leaf node. The height of an empty tree is -1, and the height of a tree with a single node is 0.

• Self-Balancing: Whenever a node is inserted, deleted, or modified in an AVL tree, the tree undergoes AVL rotations (single or double rotations) to restore the balance factor property.

• Rotations: There are four types of AVL rotations, which are performed to maintain or restore the balance of an AVL tree:

  • Left-Left (LL) Rotation
  • Right-Right (RR) Rotation
  • Left-Right (LR) Rotation
  • Right-Left (RL) Rotation

AVL Tree Operations & Implementations

For final implementation, We create an AVL Tree by extending the Binary Search Tree (BST) class. This approach allows us to implement the AVL Tree as a specialized version of the BST.

Let's explore how this is achieved and examine some of the key operations below:

• Node Structure: We define the Node structure as the basic unit of a tree, containing key, left, right, and height attributes to represent a node. The key stores the node's value, left points to the left child, right points to the right child, and height tracks the node's height. This structure enables the creation of a hierarchical data structure.

  class Node:
      def __init__(self, key):
          self.key = key
          self.left = None
          self.right = None
          self.height = 1
  

• BST Class Definition: The BST (Binary Search Tree) class is the base class for the binary search tree implementation. It has methods for standard BST operations such as insertion, searching, finding minimum and maximum elements, and deletion.

  class BST:
  def __init__(self):
      self.root = None
  
  def insert(self, key):
      self.root = self._insert(self.root, key)
  
  def _insert(self, root, key):
      if not root:
          return Node(key)
      elif key < root.key:
          root.left = self._insert(root.left, key)
      else:
          root.right = self._insert(root.right, key)
  
      return root
  
  def search(self, key):
      return self._search(self.root, key)
  
  def _search(self, root, key):
      if not root or root.key == key:
          return root
      elif key < root.key:
          return self._search(root.left, key)
      else:
          return self._search(root.right, key)
  
  def find_min(self):
      return self._find_min(self.root)
  
  def _find_min(self, root):
      if not root:
          return None
  
      current = root
      while current.left:
          current = current.left
  
      return current.key
  
  def find_max(self):
      return self._find_max(self.root)
  
  def _find_max(self, root):
      if not root:
          return None
  
      current = root
      while current.right:
          current = current.right
  
      return current.key
  
  def delete(self, key):
      self.root = self._delete(self.root, key)
  
  def _delete(self, root, key):
      if not root:
          return root
  
      if key < root.key:
          root.left = self._delete(root.left, key)
      elif key > root.key:
          root.right = self._delete(root.right, key)
      else:
          if not root.left:
              temp = root.right
              root = None
              return temp
          elif not root.right:
              temp = root.left
              root = None
              return temp
  
          temp = self._find_min(root.right)
          root.key = temp
          
          root.right = self._delete(root.right, temp)
  
      if not root:
          return root
  
     
      root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))
  
      return root
  
  def _get_height(self, node):
      if not node:
          return 0
      return node.height
  
  

• AVL Class Definition: The AVLTree class extends the BST class and implements an AVL tree, which is a specialized version of the binary search tree. It overrides the insert and delete methods to support balancing the tree after insertion and deletion.

  class AVLTree(BST):
  def insert(self, key):
      self.root = self._insert(self.root, key)
  
  def _insert(self, root, key):
      root = super()._insert(root, key)
  
      root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))
  
      balance = self._get_balance(root)
  
      if balance > 1 and key < root.left.key:
          return self._right_rotate(root)
  
      if balance < -1 and key > root.right.key:
          return self._left_rotate(root)
  
      if balance > 1 and key > root.left.key:
          root.left = self._left_rotate(root.left)
          return self._right_rotate(root)
  
      if balance < -1 and key < root.right.key:
          root.right = self._right_rotate(root.right)
          return self._left_rotate(root)
  
      return root
  
  def delete(self, key):
      self.root = self._delete(self.root, key)
  
  
  def _get_balance(self, node):
      if not node:
          return 0
      return self._get_height(node.left) - self._get_height(node.right)
  
  

• Inheritance and Method Overriding:

  • The AVLTree class inherits from the BST class to access standard BST methods and attributes.
  • The AVLTree class overrides the insert and delete methods to add AVL tree-specific behavior.
  • Defining these methods in the derived class replaces the corresponding ones from the base class.

• Method Implementations

  • Insertion:
    In BST class insertion method, a new node with a given key is added by traversing the tree recursively to find the appropriate position based on the key's value. Recursion plays a crucial role in this process as it allows the function to move down the tree, comparing the key with each node, and deciding whether to go left or right until the correct spot for insertion is found. Once the appropriate position is identified, the new node is linked to its parent, completing the insertion process in the BST.

    def _insert(self, root, key):
        if not root:
            return Node(key)
        elif key < root.key:
            root.left = self._insert(root.left, key)
        else:
            root.right = self._insert(root.right, key)
    
        return root
    

    The insert method in AVLTree class calls the BST class's insert function using super() to add the element and updates the root. It then calculates the height and balance factor of the node. Based on the balance factor and key comparisons, it performs necessary rotations for AVL balance and returns the updated root of the subtree.

    def _insert(self, root, key):
        root = super()._insert(root, key)
    
        root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))
    
        balance = self._get_balance(root)
    
        if balance > 1 and key < root.left.key:
            return self._right_rotate(root)
    
        if balance < -1 and key > root.right.key:
            return self._left_rotate(root)
    
        if balance > 1 and key > root.left.key:
            root.left = self._left_rotate(root.left)
            return self._right_rotate(root)
    
        if balance < -1 and key < root.right.key:
            root.right = self._right_rotate(root.right)
            return self._left_rotate(root)
    
        return root
        ```
    
    
    

  • Deletion:
    In BST class, the delete method uses a recursive approach to efficiently traverse the tree and find the node with the given key for deletion. After the deletion, it recursively updates the height of each node on the path from the deleted node to the root. The code also performs rotations when necessary to maintain the AVL property and balance the tree. The recursive nature of the implementation allows for concise and efficient handling of the deletion process, ensuring that the AVL property is preserved at every step.

    def _delete(self, root, key):
        if not root:
            return root
            
        if key < root.key:
            root.left = self._delete(root.left, key)
        elif key > root.key:
            root.right = self._delete(root.right, key)
        else:
            if not root.left:
                temp = root.right
                root = None
                return temp
            elif not root.right:
                temp = root.left
                root = None
                return temp
    
            temp = self._find_min(root.right)
            root.key = temp
        
            root.right = self._delete(root.right, temp)
    
        if not root:
            return root
    
        root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))
    
    return root
    

    The AVLTree class simply calls the BST class delete method.

     def delete(self, key):
        self.root = self._delete(self.root, key)
    

  • Different rotations:

    • Left-Left (LL) Rotation: Occurs when the balance factor of a node is greater than 1, and its left child has a balance factor greater than or equal to 0.

      def left_rotate(y):
          x = y.right
          T2 = x.left
      
          x.left = y
          y.right = T2
      
          y.height = 1 + max(get_height(y.left), get_height(y.right))
          x.height = 1 + max(get_height(x.left), get_height(x.right))
      
          return x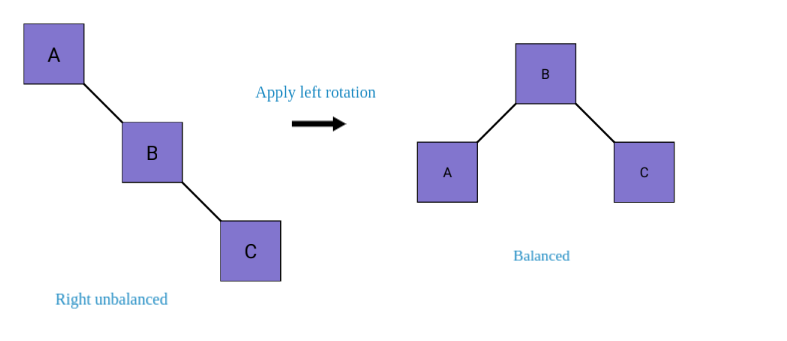
      

      

    • Right-Right (RR) Rotation: Occurs when the balance factor of a node is less than -1, and its right child has a balance factor less than or equal to 0.

      def right_rotate(x):
         y = x.left
         T2 = y.right
      
         y.right = x
         x.left = T2
      
         x.height = 1 + max(get_height(x.left), get_height(x.right))
         y.height = 1 + max(get_height(y.left), get_height(y.right))
      
         return y
      

    

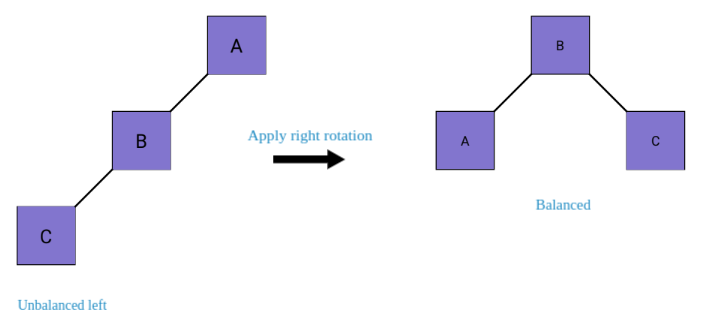
  • Left-Right (LR) Rotation: Occurs when the balance factor of a node is greater than 1, and its left child has a balance factor less than 0. It is a combination of a Left-Left (LL) and Right-Right (RR) rotation.
    

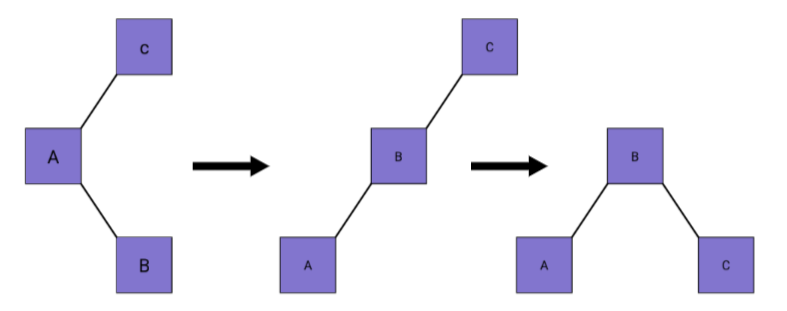
  • Right-Left (RL) Rotation: Occurs when the balance factor of a node is less than -1, and its right child has a balance factor greater than 0. It is a combination of a Right-Right (RR) and Left-Left (LL) rotation.
    

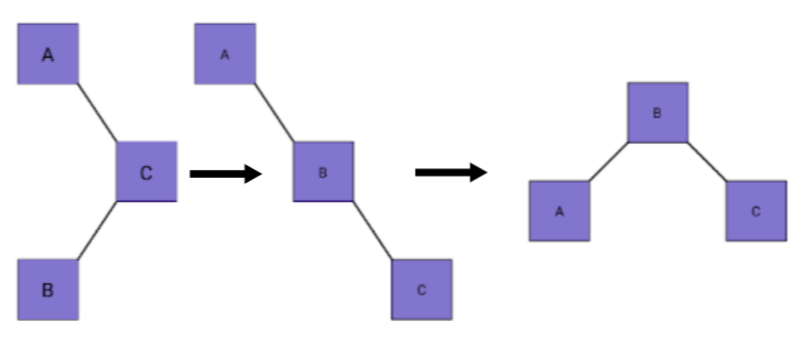
  • Searching: The search function in a binary search tree starts at the root, compares the search key with the current node's key, and proceeds left or right recursively until it finds the desired node or reaches a leaf node if the key is not in the tree. This recursive approach ensures an efficient and concise search process.

    def search(root, key):
        if not root:
            return None
    
        if root.key == key:
            return root
        elif key < root.key:
            return search(root.left, key)
        else:
            return search(root.right, key)
    

  • Minimum and Maximum:

    • Minimum: The smallest value in the tree is found in the leftmost node.

      def find_min(root):
          if not root:
              return None
      
          current = root
          while current.left:
              current = current.left
      
          return current.key
      
      

    • Maximum: The largest value in the tree is found in the rightmost node.

      def find_max(root):
          if not root:
              return None
      
          current = root
          while current.right:
              current = current.right
      
          return current.key
      

  • Helper Methods:

    • get_height: This method defined in BST class(Parent class) which returns height of a node.

      def _get_height(self, node):
      if not node:
          return 0
      return node.height
      

    • get_balance: Defines in AVlTree class(child class) that returns the balance factor of tree.

      def _get_balance(self, node):
      if not node:
          return 0
      return self._get_height(node.left) - self._get_height(node.right)
      

• Main Function and User Interaction: In main function, We creates an AVLTree object called avl_tree. Through a display_menu function, the user can interact with the tree and perform various operations such as inserting elements, searching for values, finding the minimum and maximum values, deleting elements, and exiting the program. This helps demonstrate the usage of the AVLTree class and its functionalities.

  def display_menu():
      print("AVL Tree Operations:")
      print("1. Insert")
      print("2. Search")
      print("3. Find Minimum")
      print("4. Find Maximum")
      print("5. Delete")
      print("6. Exit")
      print()
  
  
  def main():
      avl_tree = AVLTree()
  
      while True:
          display_menu()
          choice = int(input("Enter your choice: "))
  
          if choice == 1:
              key = int(input("Enter the key to insert: "))
              avl_tree.insert(key)
              print(f"{key} inserted into the AVL tree.")
  
          elif choice == 2:
              key = int(input("Enter the key to search: "))
              node = avl_tree.search(key)
              if node:
                  print(f"Node with key {key} found.")
              else:
                  print(f"Node with key {key} not found.")
  
          elif choice == 3:
              min_key = avl_tree.find_min()
              if min_key is not None:
                  print(f"The minimum element in the AVL tree is {min_key}.")
              else:
                  print("The AVL tree is empty.")
  
          elif choice == 4:
              max_key = avl_tree.find_max()
              if max_key is not None:
                  print(f"The maximum element in the AVL tree is {max_key}.")
              else:
                  print("The AVL tree is empty.")
  
          elif choice == 5:
              key = int(input("Enter the key to delete: "))
              avl_tree.delete(key)
              print(f"{key} deleted from the AVL tree.")
  
          elif choice == 6:
              print("Exiting the program.")
              break
  
          else:
              print("Invalid choice. Please try again.")
  
  
  if __name__ == "__main__":
      main()
  

Final Implementation

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1


class BST:
    def __init__(self):
        self.root = None

    def insert(self, key):
        self.root = self._insert(self.root, key)

    def _insert(self, root, key):
        if not root:
            return Node(key)
        elif key < root.key:
            root.left = self._insert(root.left, key)
        else:
            root.right = self._insert(root.right, key)

        return root

    def search(self, key):
        return self._search(self.root, key)

    def _search(self, root, key):
        if not root or root.key == key:
            return root
        elif key < root.key:
            return self._search(root.left, key)
        else:
            return self._search(root.right, key)

    def find_min(self):
        return self._find_min(self.root)

    def _find_min(self, root):
        if not root:
            return None

        current = root
        while current.left:
            current = current.left

        return current.key

    def find_max(self):
        return self._find_max(self.root)

    def _find_max(self, root):
        if not root:
            return None

        current = root
        while current.right:
            current = current.right

        return current.key

    def delete(self, key):
        self.root = self._delete(self.root, key)

    def _delete(self, root, key):
        if not root:
            return root

        if key < root.key:
            root.left = self._delete(root.left, key)
        elif key > root.key:
            root.right = self._delete(root.right, key)
        else:
            if not root.left:
                temp = root.right
                root = None
                return temp
            elif not root.right:
                temp = root.left
                root = None
                return temp

            temp = self._find_min(root.right)
            root.key = temp
            
            root.right = self._delete(root.right, temp)

        if not root:
            return root

       
        root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))

        return root

    def _get_height(self, node):
        if not node:
            return 0
        return node.height


class AVLTree(BST):
    def insert(self, key):
        self.root = self._insert(self.root, key)

    def _insert(self, root, key):
        root = super()._insert(root, key)

        root.height = 1 + max(self._get_height(root.left), self._get_height(root.right))

        balance = self._get_balance(root)

        if balance > 1 and key < root.left.key:
            return self._right_rotate(root)

        if balance < -1 and key > root.right.key:
            return self._left_rotate(root)

        if balance > 1 and key > root.left.key:
            root.left = self._left_rotate(root.left)
            return self._right_rotate(root)

        if balance < -1 and key < root.right.key:
            root.right = self._right_rotate(root.right)
            return self._left_rotate(root)

        return root

    def delete(self, key):
        self.root = self._delete(self.root, key)
    
    def _get_balance(self, node):
        if not node:
            return 0
        return self._get_height(node.left) - self._get_height(node.right)


def display_menu():
    print("AVL Tree Operations:")
    print("1. Insert")
    print("2. Search")
    print("3. Find Minimum")
    print("4. Find Maximum")
    print("5. Delete")
    print("6. Exit")
    print()


def main():
    avl_tree = AVLTree()

    while True:
        display_menu()
        choice = int(input("Enter your choice: "))

        if choice == 1:
            key = int(input("Enter the key to insert: "))
            avl_tree.insert(key)
            print(f"{key} inserted into the AVL tree.")

        elif choice == 2:
            key = int(input("Enter the key to search: "))
            node = avl_tree.search(key)
            if node:
                print(f"Node with key {key} found.")
            else:
                print(f"Node with key {key} not found.")

        elif choice == 3:
            min_key = avl_tree.find_min()
            if min_key is not None:
                print(f"The minimum element in the AVL tree is {min_key}.")
            else:
                print("The AVL tree is empty.")

        elif choice == 4:
            max_key = avl_tree.find_max()
            if max_key is not None:
                print(f"The maximum element in the AVL tree is {max_key}.")
            else:
                print("The AVL tree is empty.")

        elif choice == 5:
            key = int(input("Enter the key to delete: "))
            avl_tree.delete(key)
            print(f"{key} deleted from the AVL tree.")

        elif choice == 6:
            print("Exiting the program.")
            break

        else:
            print("Invalid choice. Please try again.")


if __name__ == "__main__":
    main()

Time and Space complexity

AVL trees are known for their efficiency due to their balanced structure, which ensures fast operations with a logarithmic time complexity of O(log n).

Additionally, the space needed to store nodes in an AVL tree is proportional to the number of elements, resulting in O(n) space complexity for nodes and O(log n) space complexity for recursion. This balance between time and space complexity makes AVL trees an ideal choice for various applications where efficient data retrieval and storage are essential.

Questions