
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained bubble sort algorithm and implemented a program on it in C Programming Language.
Table of contents
- What is Bubble sort?
- How bubble sort works
- Implementation in C Programming Language
- Output
- Explanation of C program for Bubble Sort
- Time complexity
- Drawbacks of bubble sort
What is bubble sort?
In this problem, we will be understanding bubble sort algorithm
Bubble sort is one of the most simple sorting algorithms which swaps two adjacent elements in an array if they are not in order and repeats the same procedure with the next two adjacent elements and so on.
How bubble sort works
- Suppose we have the given array
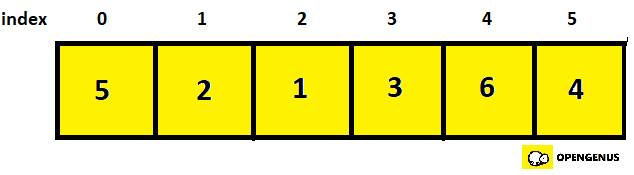
- We then create a variable named swapCounter and store the number of swaps in it.
- First we check the first two elements(element at 0th and 1st index).
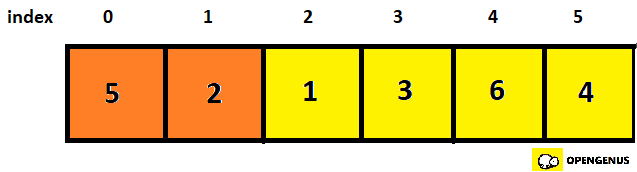
- They are not in order so we swap it and set the swapCounter to 1.
- Now we check the next two elements(element at 1st and 2nd index)
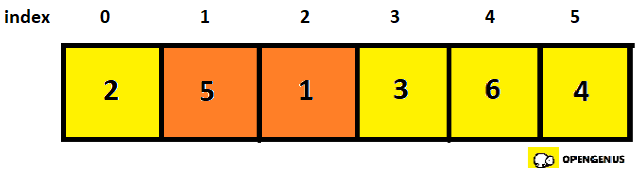
- Again they are not in order so we swap it and increment swapCounter by 1(swapCounter=2).
- Now checking the next two elements(element at 2nd and 3rd index).
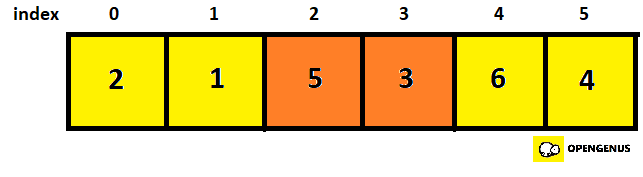
- They are not in order so we swap it and increment swapCounter by 1(swapCounter=3).
- Now checking the next two elements(element at 3rd and 4th index).
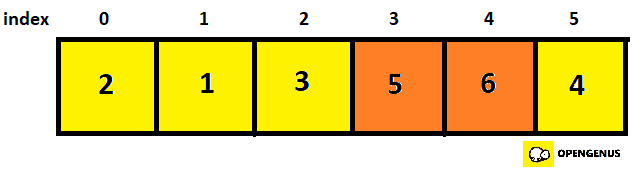
- They are in order so we don't swap it and move to the next two elements that is element at 4th and 5th index.
- They are not in order so we swap it and increment swapCounter by 1(swapCounter=4).
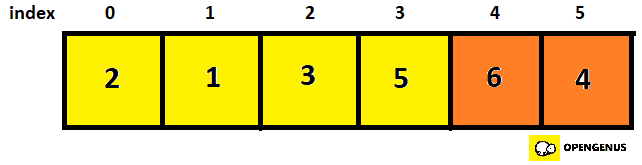
- Since we have gone through the array once, we set the swapCounter at 0 and again start checking from the 0th element
- Checking 0th and 1st element.
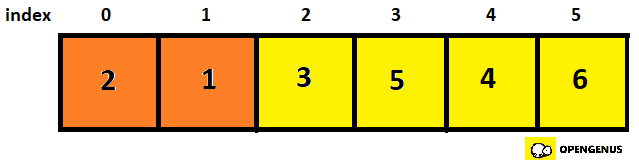
- Not in order so we swap it and set swapCounter at 1.
- Checking 1st and 2nd element.
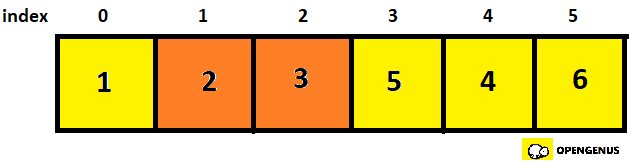
- In order, so we move to the 2nd and 3rd element.
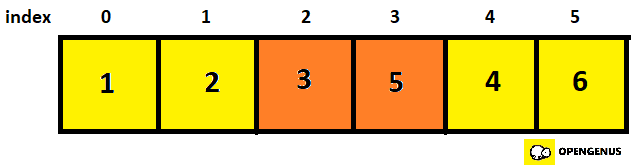
- In order, so we move to the 3rd and 4th element.
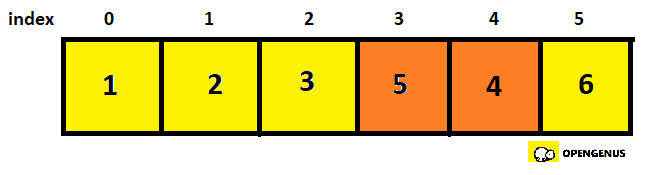
- Not in order, so we swap it and move to the 4th and 5th element.
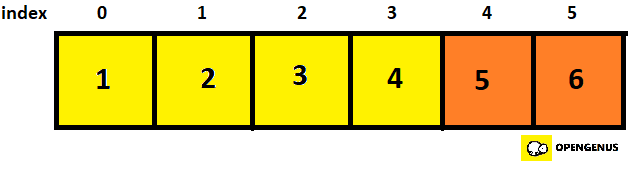
- In order
- We can see that the given array is in order now but the algorithm doesn't know this, so again checking is started from the first element by setting swapCounter to zero.
- This is where the variable swapCounter is useful, since the array is now sorted, there will be no swaps so value stored in swapCounter will be 0.
- This is when we know that the array is sorted.
Implementation in C Programming Language
Following is the implemention of the code in C programming language:
#include <stdio.h>
void swap(int* p, int* q)
{
int temp = *p;
*p = *q;
*q = temp;
}
void bubbleSort(int arr[], int n)
{
int i, j, swapCounter=0;
for (i = 0; i <= n-1 ; i++)
{
for (j = 0; j < n-1 ; j++)
{
if (arr[j] > arr[j + 1])
{
swapCounter++;
swap(&arr[j], &arr[j + 1]);
}
}
if(swapCounter==0)
break;
swapCounter=0;
}
}
void print(int arr[], int size)
{
int i;
for (i = 0; i <size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 5, 2, 1, 3, 6,4};
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: \n");
print(arr, n);
return 0;
}
Output
Run the code as follows:
gcc code.c
./a.out
Following is the output of the program:
Sorted array:
1 2 3 4 5 6
Explanation of C program for Bubble Sort
- First we enter the main function.
- Here we declare the array and store the size of the array in variable n.
- Then we call the function bubbleSort with the paraments being arr(the name of the array) and n(size of array).
- Now control goes to the function bubbleSort.
- Here we run two loops. Outer one will run throughout the length of the array and the inner one will run from 0 to less than n-1 and is used to sort the array with the condition checking if element at j>element at j+1, then the function swap is called with the parameters being the address of element at j and j+1 as it is a call by reference program.
- Now the two elements are swapped inside the function swap using a third variable.
- And the variable swapCounter is incremented by 1.
- If element at j is less than element at j+1, then no swapping occurs.
- After running through the inner loop once, it is checked if swapCounter is equal to zero or not.
- If it is equal to zero then it means that the array is sorted and breaks through the loop.
- If it is not equal, then swapCounter is initialised to zero and loop is run again till the array is sorted.
- Now the sorted array is stored in a new array in a function print and the new array is printed when the function print is called in the main function.
Time Complexity
Time complexity of bubble sort algorithm is always O(N^2) because even if the array is sorted it will always check the entire array.
Drawbacks of bubble sort
Bubble sort algorithm is not suitable for large datasets/ arrays because of its high time complexity.
