Find height or depth of a binary tree

Reading time: 20 minutes | Coding time: 5 minutes

The length of the longest path from the root of a binary tree to a leaf node is the height of the binary tree. It is, also, known as depth of a binary tree.

The height of the root is the height of the tree.

• The depth of a node is the length of the path to its root.
• We need to find the number of edges between the tree's root and its furthest leaf to compute the height of tree.

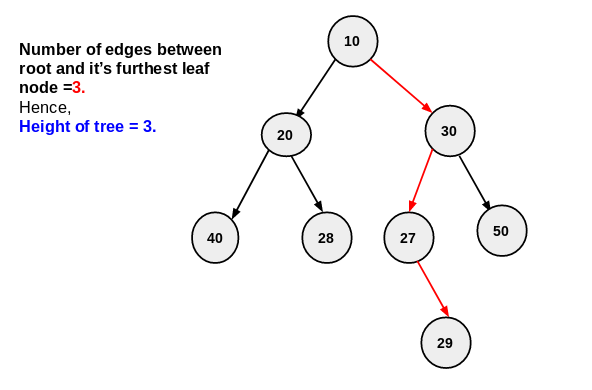
• In above example number of edges between root and furthest leaf is 3. hence height of tree is 3.

In this article we will compute the height of tree by recursively compute the height of left and right subtree and then maxium of this two is height of tree.

Steps to find height of binary tree

Following are the steps to compute the height of a binary tree:

1. If tree is empty then height of tree is 0.
2. else Start from the root and ,
   1. Find the maximum depth of left sub-tree recursively.
   2. Find the maxium depth of right sub-tree recursively.
3. Maxium depth of this two is (left and right subtree) height of binary tree.

Example :

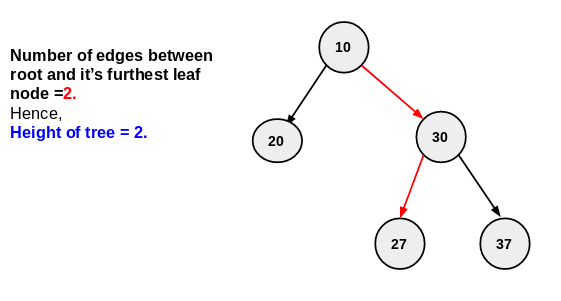
• start with root node , and recursively find maximum depth of left and right subtree .
• so our next node is 20 . 20 is leaf node . leaf node have no child . height of left subtree is 1.
• now recursively traverse to right subtree . next node is 30. 30 have both left and right node .
• first traverse to left side so next node is 27. 27 is leaf node leaf have no more child . left subtree of 30 will return 1.
• next apply same process for right subtree of node 30 . it will return 1.
• height of node 30 is 1 . number of edges between root to node 30 is 1.
  so total height of right subtree is 1+1=2.
• here height of right subtree is greater than left subtree. so height of tree=height of right subtree=2.

Pseudocode

Following is the pseudocode of the algorithm:

int height(Node root)  // return the height of tree
	{
		if(root == null)
			return -1;    
		else
		{	
            int left=height(root.left);   
            int right=height(root.right); 
             if (left > right)          
                 return left+1; 
             else
                return right+1;
		}
	}

Implementation

Following is the implementation in Java:

class Node           // construct a node for binary tree 
	{
		Node left;    //left pointer
		Node right;   //right pointer
		int data;     // key
		Node(int data)
		{
			this.data=data;
			left=null;
			right=null;
		}
	}
public class HeightOfBinaryTree 
  {
	public static int heightoftree(Node root)  // return the height of tree
	{
		if(root==null)
			return -1;    
		else
		{	
		int left=heightoftree(root.left);   // return the height of leftsubtree
		int right=heightoftree(root.right); // return the height of rightsubtree  
		 if (left>right)          // compare the height of left and right subtree
			 return left+1; 
		 else
		 	return right+1;
		}
	}
	public static void main(String[] args) 
    {		
		Node root  =new Node(10);
        root.left = new Node(20); 
        root.right = new Node(30); 
        root.left.left = new Node(40); 
        root.left.right = new Node(28); 
        root.right.left =new Node(27);
        root.right.right =new Node(50);
        root.right.left.right=new Node(29);
        System.out.println("Height of given binary tree is "+heightoftree(root));
	}

}

Output:

Height of given binary tree is 3

Complexity

Time complexity : O(n)

It is linear as we are traversing the all nodes of the binary tree recursively and maintaining the height. So, the time complexity is O(N) where N is the number of nodes in the tree.

This can be solved using Breadth First Search as well.